Modul 4 - Geometriske utfordringer

Hensikt
Matematikk
- Utforsking av vilkårlige mangekanter
- Lage diagonaler i mangekanter
- Lage mønster med linjestykker
- Beregne omkrets og areal av vilkårlige tre- og firkanter
Programmering
- Bruke kjente blokker i nye situasjoner
Oversikt over nye blokker i denne modulen
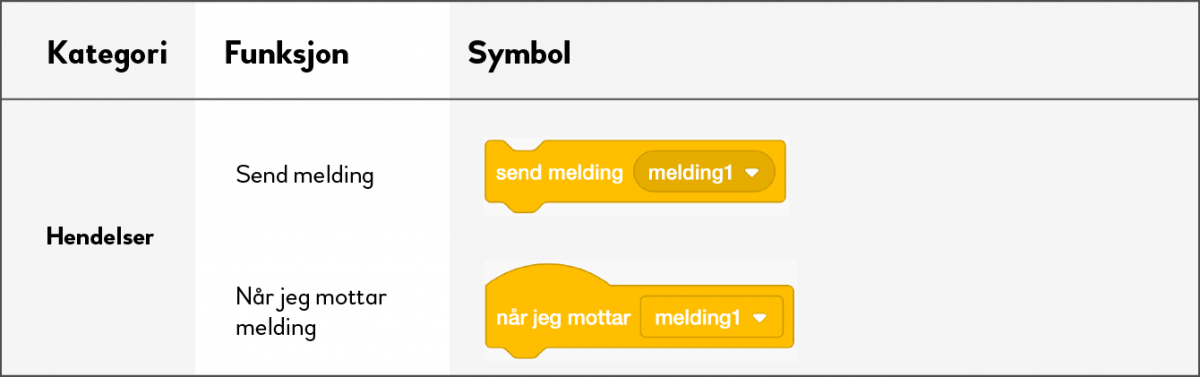
Når programmene blir lange, kan det være lurt å bryte programmet opp i to eller flere kodeblokker. Det kan man gjøre ved å sende melding fra en kodeblokk til en annen.
Kort oversikt
I denne modulen skal elevene løse alle utfordringene med blokkene som allerede er introdusert. Modulen er delt i fire deler, og DEL 1 er en oppsummering av funksjonen til kjente blokker. Dette er en analog aktivitet, og elevene bør skrive korte notater på arbeidsarket. Etter repetisjonen skal elevene utforske vilkårlige trekanter. DEL 2 handler om vilkårlige firkanter; hva kan formen bli om man går fra et vilkårlig valgt punkt via tre andre vilkårlig valgte punkter og tilbake til det første punktet? Elevene blir utfordret til å tegne diagonaler i ulike firkanter. I DEL 3 skal elevene lage mønstre med linjer i kvadrater. Elevene blir tilbudt noen ideer, men bør også skape sine egne mønstre som de skal programmere. DEL 4 dreier seg om å beregne omkrets og areal av mangekanter, og er et tillegg som bygger videre på utfordringen fra Modul 3 om å beregne avstanden mellom to tilfeldig valgte punkter i koordinatsystemet og passer derfor best for ungdomsskolen.
Del 1 - hvilke blokker kjenner du til?
Det kan være tid for å stoppe opp litt og tenke gjennom de blokkene som er benyttet til nå. Det er for eksempel nyttig å reflektere rundt likheter og forskjeller mellom blokker som har noenlunde lik funksjon og hvordan man kan sette sammen blokker.
Eksempler
Blokker som får figuren til å
- gå; gå _ steg, gå til x: _ y: _, gli _ sekunder til x: _ y: _
- rotere; snu høyre _ grader, snu venstre _ grader, pek i retning _
- sette spor; penn på, stemple avtrykk
- endre en variabel; sett (antall kanter) til _, endre (antall kanter) med _
Hvilke blokker kan man sette inn i det åpne feltet i disse to blokkene?
(arbeidsark 04a - oversikt blokker)
Vilkårlige trekanter
Elevene får se denne kodeblokken (arbeidsarkt 04b - vilkårlige trekanter):

Oppdrag til elevene:
- Hva skjer når man kjører dette programmet? Lag en kort beskrivelse.
La elevene lage beskrivelsen i par eller grupper. Oppsummer i plenum.
Her er et par spørsmål du kan bruke hvis ingen av elevene nevner dem:
- Hvorfor må man lage de to variablene x1-verdi og y1-verdi?
- Hvorfor kan man ikke bare gjenta blokken gå til tilfeldig sted, tre ganger?
La elevene lage kodeblokka og teste programmet. Be de om å vurdere om beskrivelsen deres passer til det programmet gjør.
Utforsk vilkårlige trekanter
Elevene skal kjøre programmet minst 30 ganger og notere for hver gang hvilken type trekant det ser ut til å være (arbeidsark 04c - utforsk vilkårlige trekanter). Før de starter, skal de lage en hypotese om hvilken type trekant de vil få flest ganger.
Kommentarer
For hver trekant noterer elevene hvilken type trekant det ser ut til å være.
De skal notere om trekanten ser ut til å være
- spissvinklet (alle vinklene er mindre enn 90 grader)
- stumpvinklet (én vinkel er større enn 90 grader)
- rettvinklet (hvis en vinkel er så nær 90 grader at den ser ut til å være vinkelrett)
Spørsmål å undersøke etter utprøvingen:
Hvilken type trekant kom
- flest ganger
- færrest ganger
Hvorfor er det slik?
Er det mulig at resultatet ikke blir en trekant når man kjører programmet? Hvordan kan det skje?
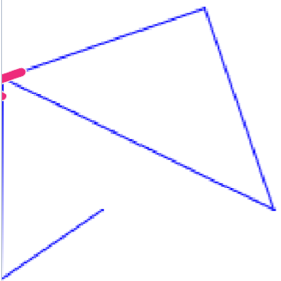
Eksempler på trekanter laget med programmet.
Med et raskt blikk kan man registrere A som rettvinklet, B som spissvinklet, C og D som stumpvinklet.
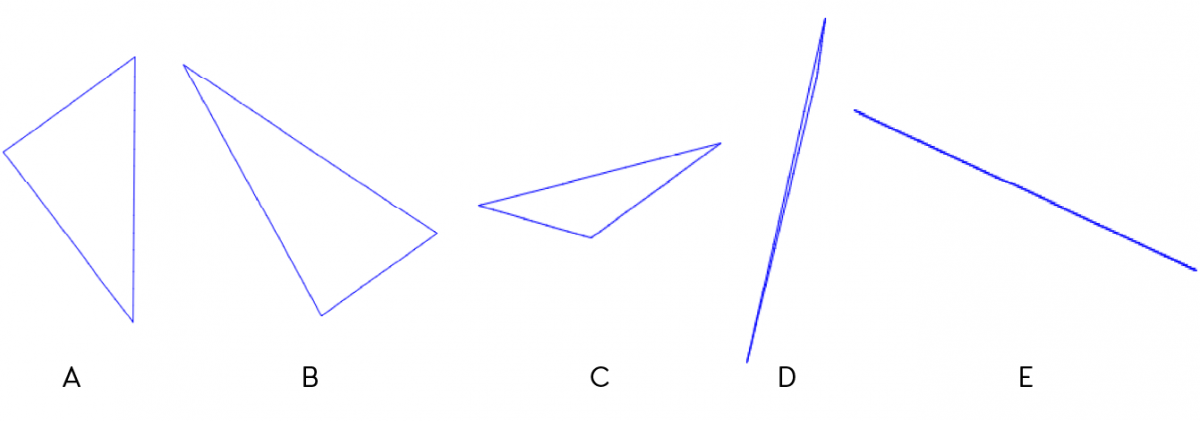
Men hva med E? Er det en trekant? Det ser ikke slik ut, og det kommer av at de tre punktene ligger på linje. Et slikt eksempel kan brukes til å utfordre elevene til å sette ord på hva som skal til for at tre tilfeldige punkter blir hjørnene i en trekant.
Del 2 - utforske vilkårlige firkanter
Elevene kan lage en kodeblokk som tegner en vilkårlig firkant ved å kopiere og endre kodeblokken som tegner en vilkårlig trekant (arbeidsark 04d - utforsk vilkårlige firkanter).
- Kjør programmet mange ganger (minst 30).
For hver figur som blir tegnet, kan dere notere om det ser ut til å være- en konveks firkant (én vinkel er større enn 180 grader)
- en konkav firkant (alle vinklene er mindre enn 180 grader)
- ingen av delene – lag da en skisse av figuren
- Hvilken type figur kom flest ganger? Hvilken kom færrest? Hvorfor er det slik?
- Er det mulig at resultatet ikke blir en firkant når man kjører progarmmet? Hvilke måter kan det skje på?
Kommentarer
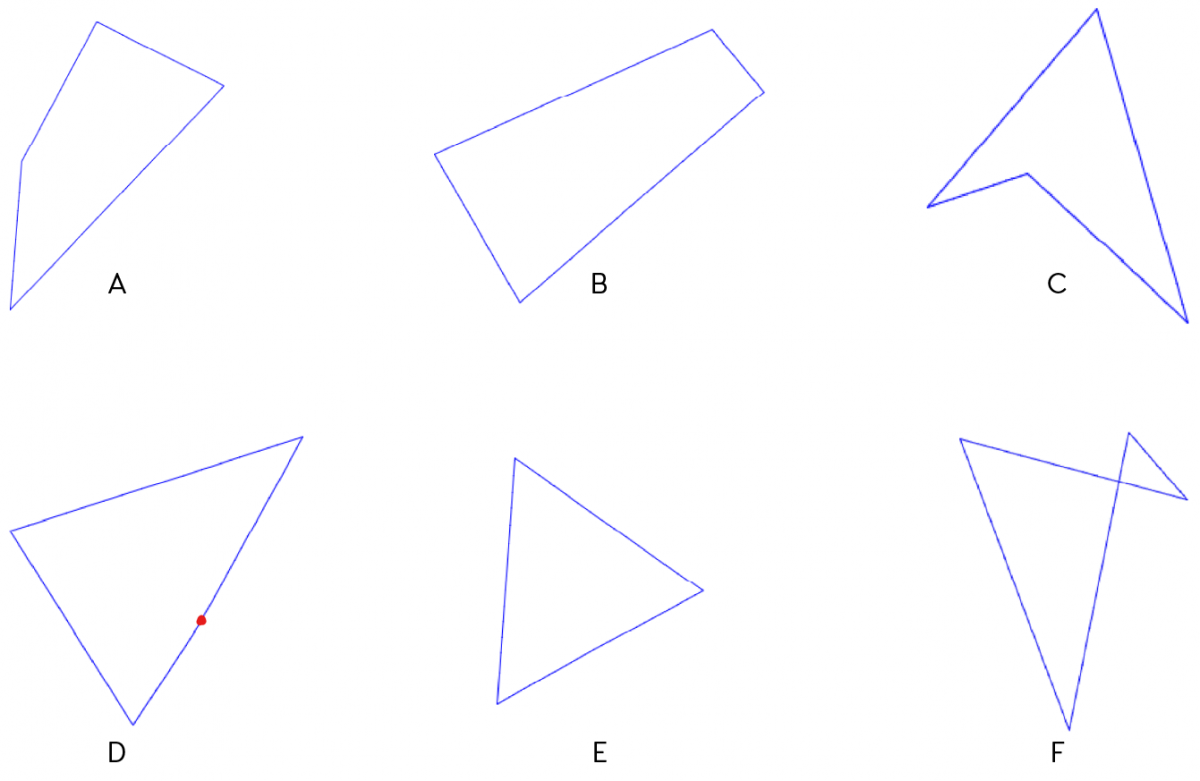
Eksemplene A-F viser "firkanter" laget med et program som tegner vilkårlige firkanter. Med et raskt blikk kan man registrere A og B som konkave firkanter og C som en konveks firkant. D og E "ser ut som" trekanter. D har et hjørne som er markert med en rød prikk. Vinkelen er svært nær 180 grader. F er ikke en firkant, men et eksempel på en firehjørnet figur.
Om man bruker figuren Ball til å lage firkantene, kan man få markert hjørnene som punkter ved å bruke blokken Stemple avtrykk i hvert hjørne.
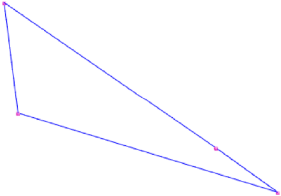
Denne mangekanten kan ved første øyekast se ut som en trekant. Siden hjørnene er markert ved å stemple avtrykk, ser vi at det er et hjørne på den ene siden. Dette hjørnet har en vinkel som er nesten 180 grader. Dersom vinkelen er nøyaktig 180 grader, så er dette en trekant.
Utfordring: Hold kontroll på firkantene
Lag program som tegner
- en konveks firkant med tilfeldige lengder på sidene.
- en konkav firkant med tilfeldige lengder på sidene.
Diagonaler i kvadrater
I modul 3 laget dere et program som tegnet et kvadrat med en diagonal. Programmet kan se slik ut (arbeidsark 04e - kvadrat med diagonal):
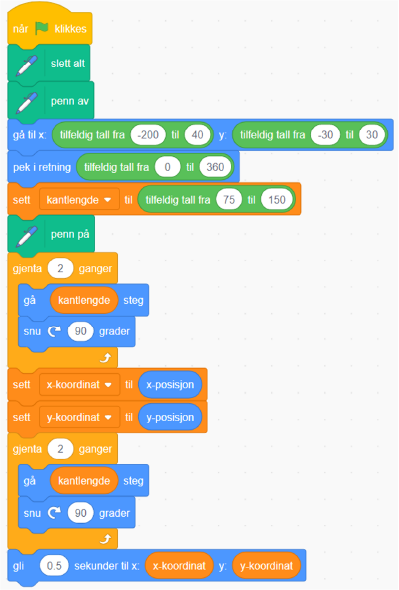
- Studer programmet. Forklar hvorfor det tegner et kvadrat med en diagonal.
- Lag programmet og kjør det minst ti ganger. Får du alltid et kvadrat med en diagonal? Hvis ikke, gjør endringer slik at du alltid får et kvadrat med en diagonal.
- Gjør endringer i programmet slik at det tegner et kvadrat med begge diagonalene.
Kommentar
Hvis figuren går utenfor resultatvinduet, blir figuren ødelagt. Da kan man begrense tilfeldigheten ved å endre verdier i en eller flere av operasjonsblokkene tilfeldig tall fra _ til_.
Diagonaler i firkanter
La elevene prøve seg på å lage programmer som tegner
- et rektangel med diagonaler
- et parallellogram med diagonaler
- en rombe med diagonaler
- en vilkårlig firkant med diagonaler
Del 3 - linjemønster i kvadrater
Dette programmet er satt sammen av to kodeblokker. Når programmet blir laget med mange blokker, kan det bli mer oversiktlig å dele programmet opp i to eller flere kodeblokker.
Eksempel
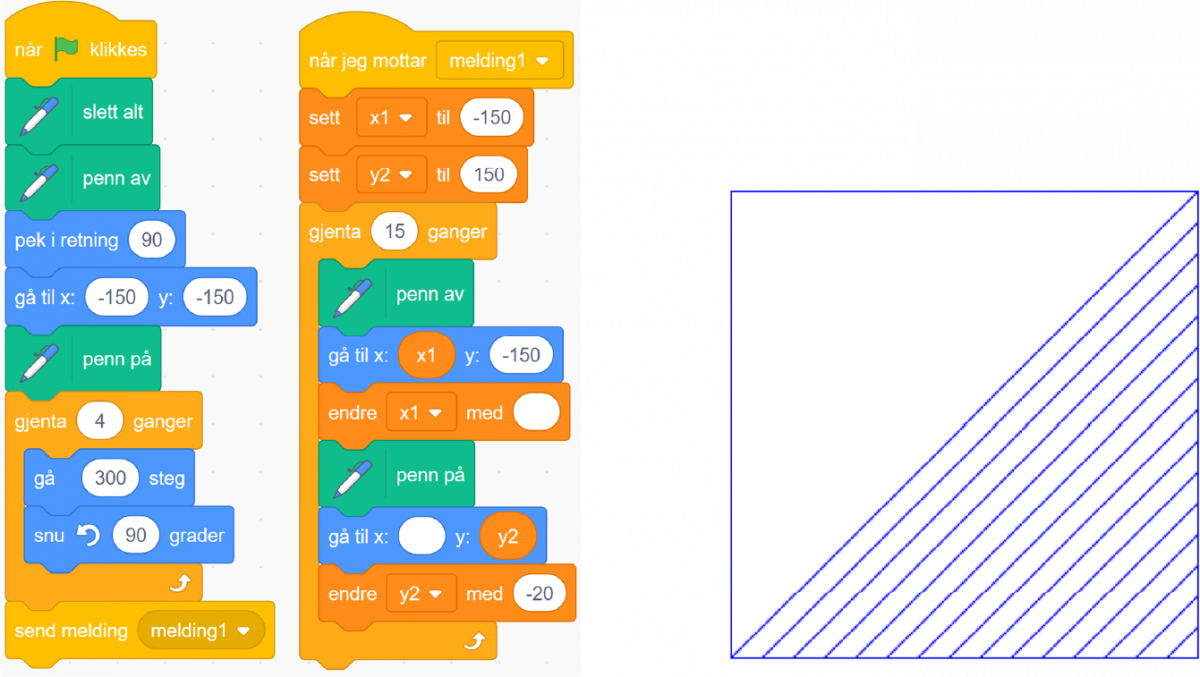
Eksemplet viser et program som lager linjer i et kvadrat (arbeidsark 04f - linjer i kvadrat).
- Se nøye på programmet.
- Hvilke blokker er brukt for å sette disse to kodeblokkene sammen til ett program?
- Hva skjer med variablene x1 og y2 når programmet kjøres?
- To blokker har et tomt felt der det skal stå tall. Hvilke tall må stå i hver av de to blokkene?
- Lag en skisse av mønsteret programmet tegner.
- Lag programmet og sjekk om tallene dere velger lager et mønster i et kvadrat.
Ideer til mønster dere kan lage
Ideene er samlet i arbeidsark 04g - ideer til mønster.

Stjerner
Stjerner kan lages på to forskjellige måter. Med diagonaler:
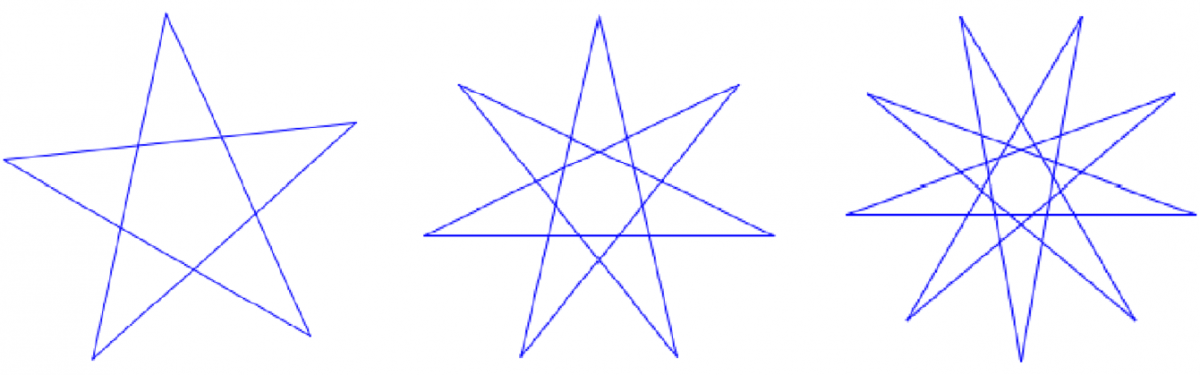
Med omrisset av stjernen

Del 4 - avstand mellom punkter
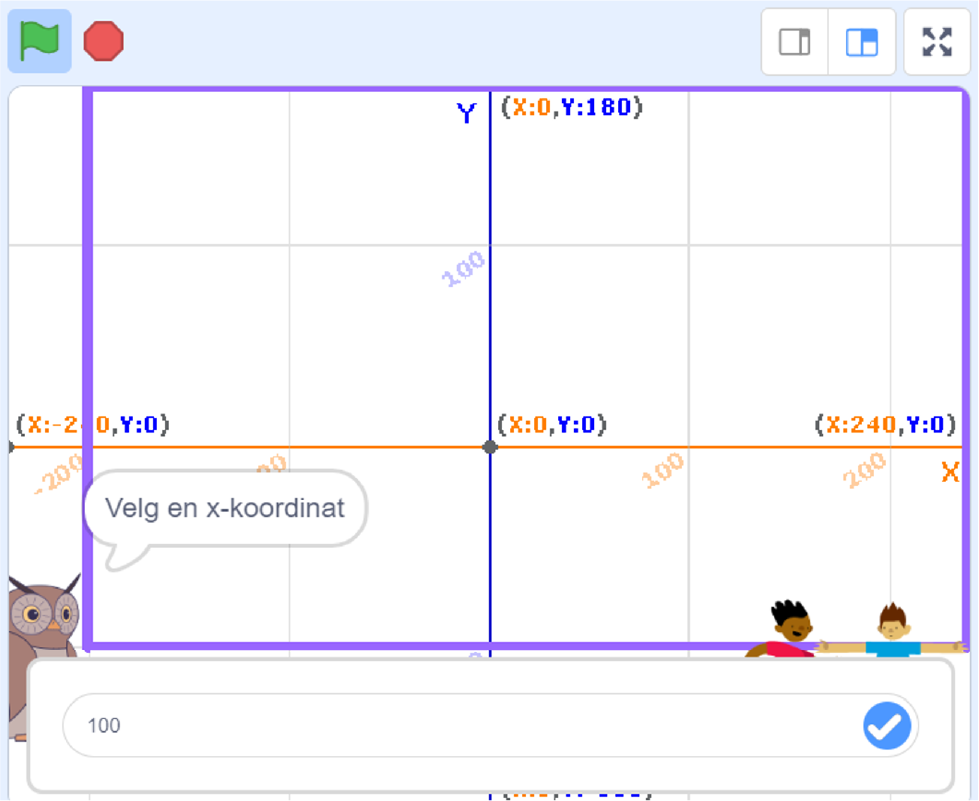
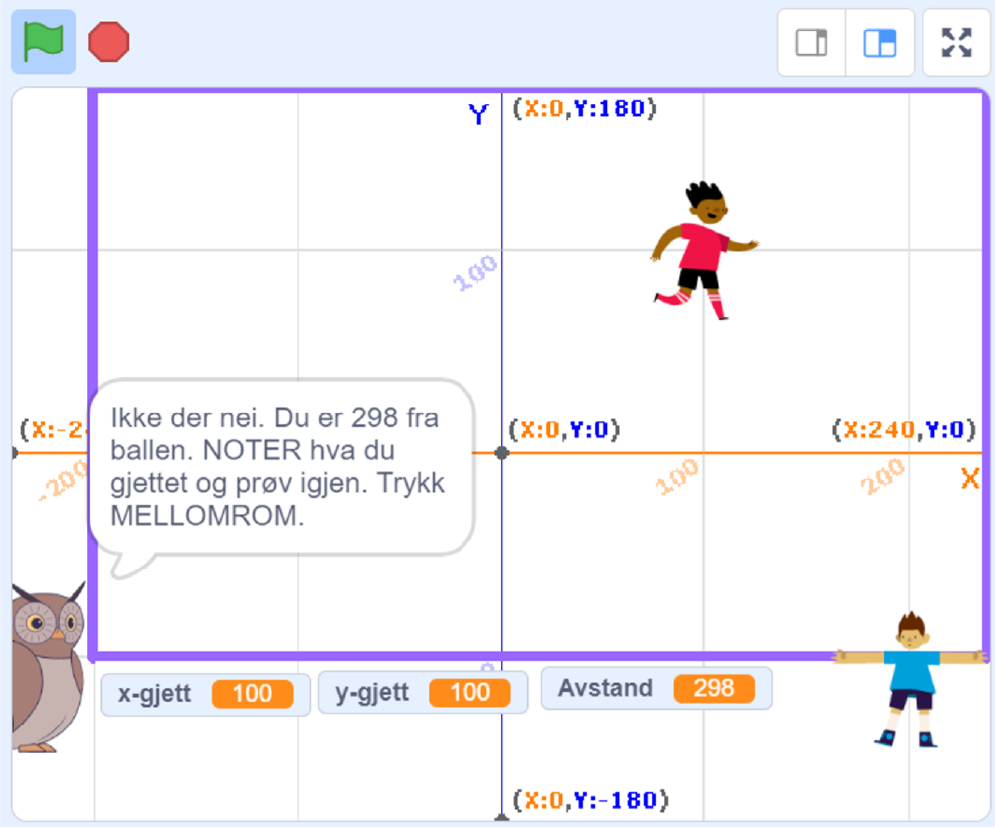
Programmet skal beregne avstanden mellom to tilfeldig valgte punkt.
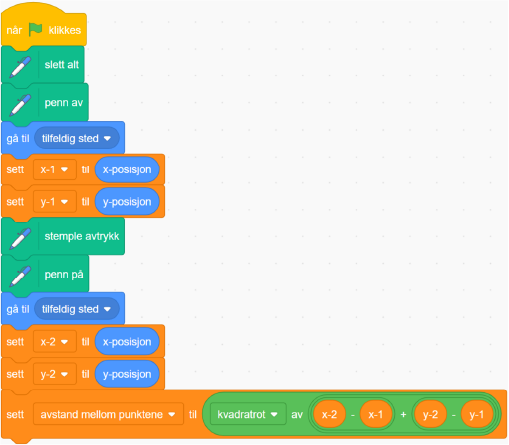
En test av programmet ga noen merkelige resultat:

Undersøk programmet og gjør nødvendige endringer (arbeidsark 04h - avstand mellom punkter).
Beregne omkrets av trekanter
Lag et program som beregner omkretsen til en vilkårlig trekant.
Arealberegning
- Lag et program som beregner arealet til en vilkårlig trekant.
Hint: Herons formel bruker kun lengden til sidene i en trekant for å beregne arealet til trekanten:- Beregn først omkretsen til trekanten og divider denne på to: `s=O / 2`
- Arealet til trekanten kan da beregnes med denne formelen:
`A=root(2)(s(s-a)(s-b)(s-c))`
- Lag programmer som tegner og beregner lengden til diagonalene i
- et kvadrat med tilfeldige sidelengder
- et parallellogram med tilfeldige sidelengder
- en rombe me tilfeldige sidelengder
- en vilkårlig konkav firkant med tilfeldige sidelengder
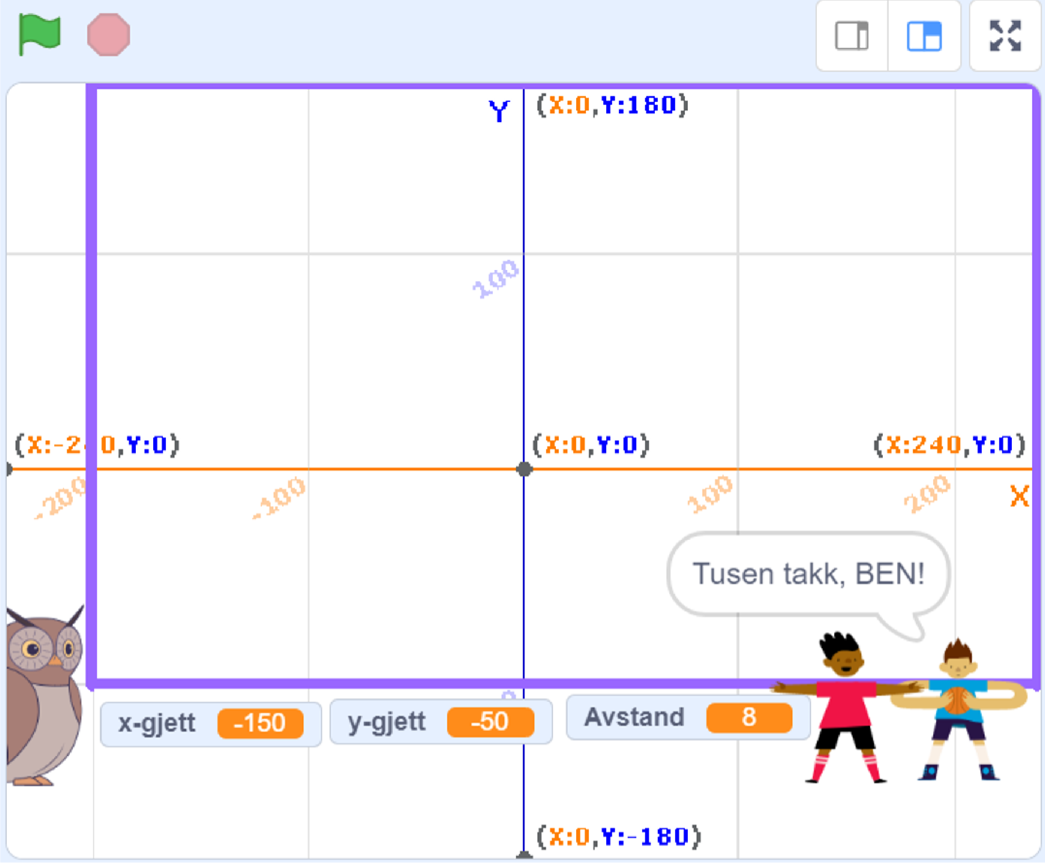
Prøv deg på et spill
Eksempel
Finn ballen! – Hvem klarer det på færrest forsøk?