Puslespill seilbåt
Emne
Multiplikativ tenking (proporsjonalitet, målestokk, forstørring, brøk som operator).
Aktiviteten er hentet fra Kartlegging av matematikkforståelse. Introduksjon til diagnostisk undervisning i matematikk (Brekke, 2002).
Hensikt
Elevene skal finne og uttrykke sammenhengen mellom tallstørrelser, og at de kan bruke brøk til å beskrive forholdet mellom ulike sider i en figur.
Aktiviteten gir mulighet til å observere om elevene identifiserer en multiplikativ sammenheng. Elever som tenker additivt i denne oppgaven (adderer 2 til alle lengdene), vil se at det nye puslespillet får en annen form enn utgangspunktet. Misoppfatningen kommer til syne, slik at elevene kan diskutere eller reflektere omkring den. Oppgaven er et eksempel på en aktivitet som vil skape en kognitiv konflikt.
Valg av tidspunkt
Du trenger
Elevark Seilbåt. Sakser. Ark og lim.
Elevark Fly dersom det er ønskelig.
Aktiviteten
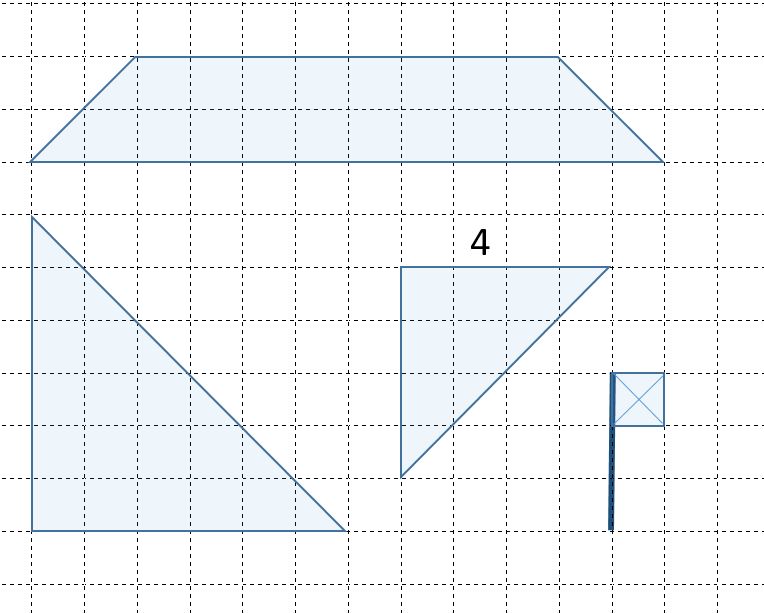
I denne aktiviteten skal elevene forstørre et puslespill. Elevene arbeider sammen i par og får utdelt en kopiorginal med puslebrikker. Elevene skal klippe ut bitene og sette dem sammen til en seilbåt. Bitene kan med fordel limes på et ark.Deretter skal elevene forstørre bitene, klippe de ut og sette de sammen til en ny seilbåt.Et alternativ er å arbeide med puslespillet Fly. Matematikken er den samme i de to aktivitetene.
Oppgave 1 til elevene
Klipp ut bitene som er tegnet på side to. Sett bitene sammen til en seilbåt.
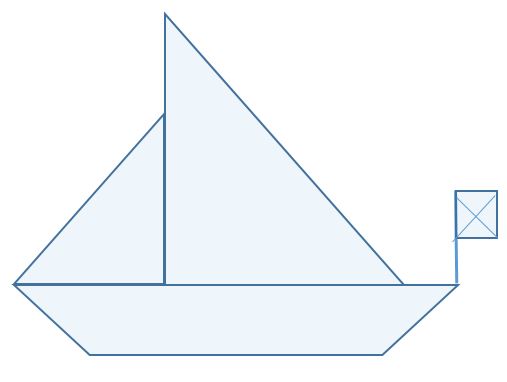
Dere kan gjerne lime bitene på et ark. Når bitene er satt sammen vil seilbåten se slik ut:
Oppgave 2 til elevene
Dere skal forstørre seilbåten. Sidenkanten som har lengde 4, skal få lengde 6.
- Forstørr alle de andre bitene på tilsvarende måte, og tegn de nye bitene på side tre.
- Klipp ut de nye bitene dere har laget og lag seilbåten. Dere kan gjerne lime bitene på et ark.
- Skriv ned det dere gjorde.
Diskuter
- Er den nye seilbåten lik den opprinnelige? Forklar og begrunn.
- Dersom de ikke har samme form, hva kan årsaken være?
- Hvordan tenkte dere da dere lagde bitene til den nye seilbåten?
Oppgave 3 til elevene
Dere skal nå lage en ny seilbåt. Sidenkanten som har lengde 4, skal få lengde 8.
- Forstørr alle de andre bitene på tilsvarende måte, og tegn de på side fire.
- Klipp ut bitene og lag den nye seilbåten. Dere kan gjerne lime bitene på et ark.
- Skriv ned det dere gjorde.
Diskuter
- Hvordan ser den nye seilbåten ut sammenlignet med de to forrige?
- Tenkte dere på samme måte som i oppgave 2, da dere lagde bitene til denne seilbåten? Forklar og begrunn.
Kommentarer til opplegget
Det er meningen at aktiviteten skal skape en diskusjon for å rydde eventuelle misoppfatninger av vegen. Dersom noen elever har en bestemt misoppfatning, vil aktiviteten bringe misoppfatningen fram i dagen. I denne aktiviteten møter elevene problemstillinger knyttet til begrepene forskjell og forhold. Selv om de fleste elever løser denne oppgaven uten å relatere det til brøk, vil oppgaven avsløre om elevene gjenkjenner den multiplikative sammenhengen. Elever som tenker additivt vil addere 2 til alle lengdene, i stedet for å multiplisere med `(3)/(2)`. De vil gjennom å lage bitene, klippe de ut og sette de sammen, erfare at den nye seilbåten får en annen form enn den opprinnelige.
Denne tenkingen kan henge sammen med misoppfatningen om at størrelsen til en brøk vurderes ut fra differensen mellom teller og nevner, i stedet for å se på forholdet mellom teller og nevner.
Multiplikativ tenking (i dette eksemplet en forstørring):
- Sidekanten som har lengde 4 skal få lengde 6.
- Oppgaven er å skal lage en forstørring av bitene. Ved å sammenligne de to sidekantene, ser vi at forholdet mellom de er `(6)/(4)` eller`(3)/(2)`. Alle sidekantene må multipliseres med `(3)/(2)`.
- I den den største trekanten har sidekanten lengde 6.
- I en forstørret utgave av denne trekanten blir tilsvarende lengde 6 ∙ `(3)/(2)` = 9
Den pedagogiske utfordringen her kan være at elever som ikke identifiserer den multiplikative sammenhengen, heller ikke ser noen annen løsning enn å addere to til alle mål. De vil se at den nye seilbåten ikke ligner på den de startet med. Noen elever tror at forstørring betyr å lage hver bit større, uten å ha skjønt den matematiske ideen knyttet til forstørring, nemlig at formen skal være den samme etter forstørringen. Målet må være at elevene forstår at dette ikke skjer ved å addere en fast størrelse til alle målene. Elevene må erfare og forstå at formen ikke blir den samme ved additiv tenking. Det å se at seilbåten som er forstørret ikke ligner på den opprinnelige, skaper en slik konfliktsituasjon og er viktig for videre læring.
Forslag til utvidelse
Læreren kan be elevene lage en ny seilbåt der sidekanten som er 4, skal få lengde 8. Mange elever vil trolig doble alle mål og få en seilbåt som er en korrekt forstørring av den opprinnelige seilbåten. Disse to aktivitetene til sammen vil være et godt utgangspunkt for diskusjon og refleksjon som retter fokus mot misoppfatningen, og gir elevene mulighet til å vurdere egen tenkning. Etter å ha skapt en kognitiv konflikt hos elevene, må elevene få støtte og veiledning slik at de kommer ut av konflikten. En løsningsfase, hvor diskusjoner og refleksjoner omkring det en har funnet ut, er helt sentralt.
Rammeplanmål/Kompetansemål
- Grunnskole
- Kompetansemål etter 5. trinn
- utvikle og bruke ulike strategiar for rekning med positive tal og brøk og forklare tenkjemåtane sine
- Kompetansemål etter 6. trinn
- bruke variablar og formlar til å uttrykkje samanhengar i praktiske situasjonar