Oppgavestreng 198 + 7
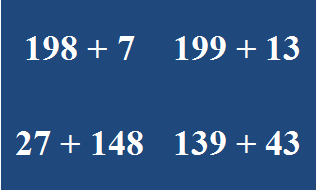
Emne
Utvikle effektive strategier i arbeid med tall og regneoperasjoner.
Begrunne strategier på enkelteksempler.
Dette opplegget er utviklet som en del av MAM-prosjektet.
Hensikt
Utnytte vennlige tall i hoderegning ved å opprettholde lik verdi.
Bruke ulike representasjoner av tall og regneoperasjoner.
Valg av tidspunkt
Du trenger
Tavle.
Aktiviteten
Læreren skriver en og en oppgave på tavla. Når de fleste elevene viser at de har tenkt ferdig, spør læreren hvordan de kom fram til svaret. Læreren noterer elevenes tenkemåte med symbolsk notasjon og en representasjon og leder diskusjonen om de ulike strategiene. I diskusjonen fremhever læreren strategien der man utnytter de to første regnestykkene i arbeid med de to siste.
I de to første oppgavene er tallene valgt slik at det faller naturlig å fylle opp de første tallene til nærmeste hundrer ved å ta fra det andre tallet. I de to siste oppgavene er det like naturlig å fylle opp til nærmeste tier. I den tredje oppgaven er det flest enere i det siste tallet, for å se om elevene vurderer tallene.
Det kan være en idé å spare på notatet slik at det kan brukes senere. Elevene bør bli oppmerksomme på og reflektere over hva andre sier. Gi elevene tid til å tenke. Mer om aktiviteten oppgavestrenger finner du på nettsiden til MAM-prosjektet.
Matematiske sammenhenger
Matematiske sammenhenger 
Hensikten med aktiviteten er at elevene skal utvikle hensiktsmessige strategier i arbeid med addisjon. Mer spesielt, oppgavestrengen fremhever bruk av vennlige tall som en strategi i arbeid med addisjon,
198 + 7 = 198 + (2 + 5) = (198 + 2) + 5 = 200 + 5
198 + 7 = (198 + 2) + (7 – 2) = 200 + 5
Et av målene med aktiviteten er at den gitte strategien skal begrunnes på de gitte eksemplene. Ulike representasjoner av tall og regneoperasjoner vil være nødvendige i denne sammenhengen.
Vurdering av tall og valg av hensiktsmessig strategi
Denne oppgavestrengen bygger på at elevene kan se et tall på ulike måter. For eksempel kan tallet 198 betraktes som 190 + 8, 100 + 98 osv. Denne oppgavestrengen oppfordrer elevene til å se 198 som 200 – 2. Dette gir mulighet til å regne med 200 som er et «vennligere» tall. Å vurdere en multiplikasjon med tanke på å finne «vennligere» tall å regne med, vil kunne forenkle regneprosessen i mange tilfeller. Kunnskap om egenskaper ved de involverte tallene og regneoperasjonen i et gitt regnestykke, gjør elevene i stand til å velge strategier som både er effektive og nøyaktige.
Ulike representasjoner av addisjon og overganger mellom dem
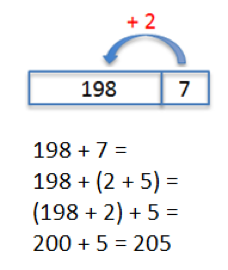 Målet med samtalen er strategien der man ser addendene som en sum eller en differanse. Strategien bør beskrives muntlig, med matematiske symboler og med en illustrasjon eller en regnefortelling. Når man skal begrunne hvorfor strategien er en gyldig framgangsmåte, er det nødvendig å gi mening til addisjonen gjennom en regnefortelling eller en illustrasjon.
Målet med samtalen er strategien der man ser addendene som en sum eller en differanse. Strategien bør beskrives muntlig, med matematiske symboler og med en illustrasjon eller en regnefortelling. Når man skal begrunne hvorfor strategien er en gyldig framgangsmåte, er det nødvendig å gi mening til addisjonen gjennom en regnefortelling eller en illustrasjon.
Det er viktig å være oppmerksom på at de ulike representasjonene av strategien kobles sammen, at man følger det som skjer både symbolsk, muntlig og gjennom illustrasjonen eller regnefortellingen.
Varierte strategier i addisjon
I oppgaven 198 + 7 vil enkelte elever telle opp fra 198 – 199 – 200 – … – 205, og gjerne bruke fingrene som hjelp til å holde orden på hvor mange de skal legge til. Etter hvert som elevene har forståelse for posisjonssystemet vil de utnytte det i addisjonen.
I oppgaven 27 + 148 vil det bli vanskeligere å holde styr på telling og fingre om en skal telle oppover med enere, selv om enn starter fra 148. Enkelte elever vil her kombinere enere og tiere og for eksempel tenke en hundrer, fire tiere og to tiere er seks tiere, åtte enere og sju enere er femten enere som igjen er en tier og fem enere. De ser dette for seg i hodet og holder styr på enere, tiere og hundrere og omgrupperer slik at de kommer fram til svaret.
Andre elever vil bruke trinnvis økning ved å dele opp 27 i tiere og enere og regne videre fra 148. Å regne med hele tiere er enda enklere, og dersom elevene utnytter dette kan de legge til 30 og trekker fra tre.
Hensikten med oppgavestrengen er å få elevene til å se at en mengde kan deles i ulike delmengder uten at hele mengden blir endret og utnytte det i hoderegning ved å gjøre tallene i et addisjonstykke vennligere og lettere å regne med. Ved å flytte 2 fra 27 til 148, blir regnestykket 150 + 25 i stedet for 148 + 27.
Begrunne strategien på de gitte regnestykkene
Man kan modellere regnestykkene på ulike måter.
Oppgaven 198 + 7 kan modelleres med for eksempel med klinkekuler, en figur eller tallinje.
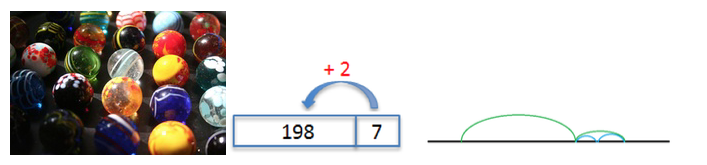
I en modell kan dette illustreres med at man flytter kuler mellom posene uten at det totale antall kuler forandrer seg. Det er viktig å kombinere modellen med muntlig språk og symbolsk notasjon, slik at elevene forstår de regneoperasjonene de utfører.
Rammeplanmål/Kompetansemål
- Grunnskole
- Kompetansemål etter 3. trinn
- utforske og forklare samanhengar mellom addisjon og subtraksjon og bruke det i hovudrekning og problemløysing
