Oppgavestreng: Divisjon med desimaltall

Divisjon med desimaltall. Mønster og sammenhenger i divisjon.            

Dette opplegget er utviklet som en del av MAM-prosjektet.

Tavle.

Læreren starter med å fortelle om Stian som har en kalkulator som er ødelagt slik at desimalkomma ikke vises på skjermen. Når Stian slår inn 249 : 7, får han 35571 som siffer på skjermen. Skjermen på kalkulatoren viser riktige siffer, men angir svaret uten desimalkomma. Hvor skal desimalkommaet stå?

Læreren skriver den første oppgaven på tavla, og sifrene som Stian fikk på kalkulatoren. Elevene får tenketid, før de kommer med forslag om hvor de vil plassere desimalkommaet.  Når de fleste elevene viser at de har tenkt ferdig, spør læreren hvordan de kom fram til svaret.

Deretter presenterer læreren de neste oppgavene, en etter en, og elevene begrunner sine svar og argumenterer for sine løsninger. 

Læreren noterer elevenes tenkemåte og leder diskusjonen om de ulike strategiene. I diskusjonen fremhever læreren strategien der man utnytter relasjonen mellom dividendene og mellom divisorene. Læreren utfordrer elevene på å bruke svarene og resonnementene fra de foregående oppgavene til å forstå og forklare hva som skjer når verdiene i dividend og divisor endres.

Læreren må være bevisst på å snakke om å gjøre tallet ti ganger større/mindre og at sifrene endrer verdi i stedet for å bruke betegnelsen «å flytte komma». Det kan være en idé å spare på notatet slik at det kan brukes senere.

I vedlagte undervisningsnotat er det forslag til en progresjon for gjennomføring og retning for en diskusjon som fremmer de faglige målene. Læreren bør bruke samtaletrekkene slik at elevene blir oppmerksomme på og reflekterer over hva andre sier. Elevene må få tid til å tenke.

Matematiske sammenhenger

Posisjonssystemet

Oppgavestrengen gir en mulighet til å diskutere posisjonssystemet og desimaltall. Mange elever bruker begreper som å flytte komma, legge til eller fjerne nuller når det er snakk om å gjøre tall ti ganger større eller ti ganger mindre. Noen bruker disse begrepene og har forståelse for posisjonssystemet og hvordan verdien av sifrene endres, men mange reflekterer ikke over hva som egentlig skjer. I arbeidet med denne oppgavestrengen utfordres forståelsen for posisjonssystemet. Sifrenes verdi i 35571 avhenger av hvor elevene plasserer desimalkommaet.

Overslagsregning

I denne sekvensen knytter vi divisjon til overslagsregning. Det krever at elevene kjenner divisjon som regneart, og at de også er i stand til å se sammenhengen mellom divisjon og multiplikasjon. Når elevene skal vurdere hvor desimalkommaet skal stå i 249 : 7, ser de at svaret må bli større enn 3,5571 men mindre enn 355,71 fordi 3 · 7 er mye mindre enn 249, og 355 · 7 er mye mer enn 249. Ved å knytte divisjonsforståelse til overslagsregning, kan det kanskje gi elevene flere strategier til å vurdere svar i praktiske oppgaver med desimalkomma, eller når man foretar beregninger med en kalkulator.

Begrunnelser

I denne strengen har vi valgt å gå på begrunnelser ut fra posisjonssystemet og overslagsregning. Når vi skal begrunne hvorfor divisjon med 7 gir et svar som er ti ganger større enn divisjon med 70, er det viktig å betrakte tallet 7 som ti ganger mindre enn 70. Skal man gå dypere inn i begrunnelsen hvorfor det skjer, kan man illustrere divisjon gjennom en regnefortelling (målingsdivisjon) eller på en tallinje som vist. Her kan regnefortellingen være at du har en planke på 249 cm som skal deles i biter på 7 cm eller biter på 70 cm. Hvor mange får du?

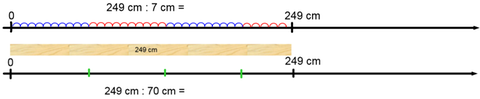
Når man går videre i denne oppgavestrengen er ikke målet å få vist representasjonen med alle regnestykkene, men heller å bruke den kunnskapen man får i de to første oppgavene i strengen til å resonnere hvordan svaret må bli i de etterfølgende oppgavene.

249 : 7 = 35,571    og  249 : 70 = 3,5571