Telle i kor med 120 fra 120
Emne
Beskrive, bruke og begrunne mønstre og sammenhenger.
Dette opplegget er utviklet som en del av MAM-prosjektet.
Hensikt
Beskrive egenskaper ved tallene. Se hvordan sifrene på tier- og hundrerplass øker. Finne økning fra kolonne til kolonne i samme rad.
Valg av tidspunkt
Du trenger
Tavle, gjerne interaktiv tavle, eller flippover.
Aktiviteten
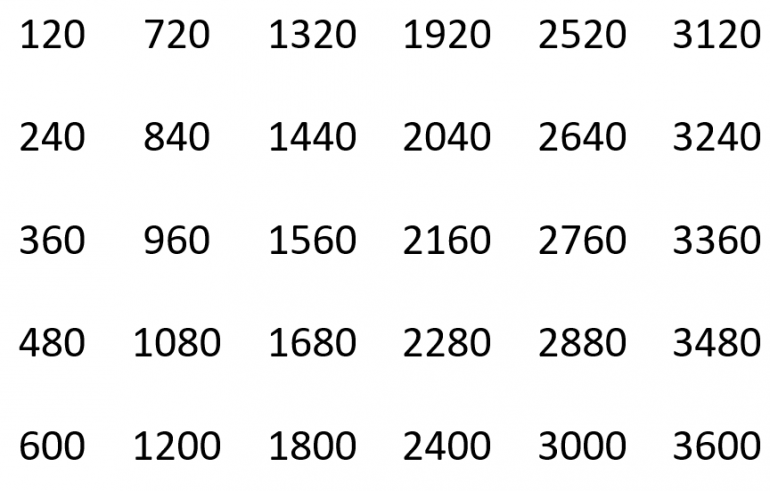
Tellingen starter på 120 og vi teller med 120 om gangen. Skriv tallene i kolonner på fem. Det kan være til hjelp å lage et tomt rutenett på forhånd. Skriv tallet 120 og gi elevene tid til å tenke ut de neste tallene. Elevene sier tallene i kor samtidig som læreren skriver tallet.
Tabellen fylles ut under tellingen og, elevene beskriver hvordan de bruker mønstre og sammenhenger til å finne tallene. Noter elevenes forslag og marker mønstre og sammenhenger i tabellen. Det kan være en idé å spare tabellen med notater slik at den kan brukes igjen senere.
De matematiske sammenhengene i opplegget «Telle med 120 fra 120» blir drøftet nærmere nedenfor.
Elevene bør bli oppmerksomme på, og reflektere over hva andre sier. Gi elevene tid til å tenke. Mer om Telle-i-kor-aktiviteter finner du her.
I undervisningsnotat til læreren ligger det forslag til videreføring av opplegget. Del 1 av opplegget kan være mulig å gjennomføre på ca. 15 min.
Matematiske sammenhenger
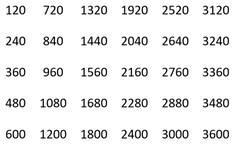
Tellingen starter på 120 og øker med 120, og vi får egentlig en multiplikasjonstabell for 120. Når vi går nedover i en kolonne øker vi 120 fra rad til rad. Hopper vi over en rad er økningen 2 · 120 = 240, hopper vi over to rader blir økningen 3 · 120 = 360 osv.
Med fem tall i hver kolonne får vi en forskjell på 5 · 120 = 600 mellom naboruter i to kolonner. Hopper vi over to kolonner vil økingen bli 1200 osv. Sifferet på 100-plassen øker med 1 på de fire første tallene, så hopper vi over 5 og går fra 480 til 600. Det er fordi fem 20-ere utgjør en ny hundrer. Tilsvarende mønster får vi mellom de to siste tallene i hver kolonne.
På 10-erplassen finner vi mønsteret 2 – 4 – 6 – 8 – 0 ovenfra og ned i hver kolonne. Det betyr også at vi får samme siffer på 10-erplassen i en rad. Sammen med økningen på 600 fra kolonne til kolonne kan dette være en nyttig informasjon å resonnere ut fra når elevene skal finne ut om et bestemt tall (4520) vil komme et eller annet sted i tabellen. Tallet må eventuelt komme i øverste rad, men økningen fra 3120 til 4520 er 1400, og det går ikke opp i 600.
Vi kan også gå på «skrå», f.eks. fra 2040 til 2760, ved å legge til 720. Vi går da først en kolonne til høyre, legger til 600, og en rad ned, legger til 120 – eller i motsatt rekkefølge. Det er også mulig å gå en rad opp. Da må vi subtrahere 120. Alle mønstrene stammer fra strukturen i tabellen som er telling med 120 skrevet i kolonner på fem.
Siden tabellen er en multiplikasjonstabell for 120, finner vi for eksempel 13 · 120 = 1560 i tredje rute i tredje kolonne. I de to første kolonnene har vi multiplisert 120 med tallene 1-10.
13 kommer som tredje tall i tredje kolonne.
Alle tall i tabellen kan skrives på formen 120 · n.
Vi kan finne et nytt tall i tabellen ved å addere to tall som allerede er riktig plassert:
2160 = 18 · 120 og 3240 = 27 · 120.
2160 + 3240 = 5400 vil komme i tabellen.
Tallet hører hjemme i rute nummer 45: 18 · 120 + 27 · 120 = (18 + 27) · 120 = 45 · 120.
Rammeplanmål/Kompetansemål
- Grunnskole
- Kompetansemål etter 5. trinn
- utvikle og bruke ulike strategiar for rekning med positive tal og brøk og forklare tenkjemåtane sine
