1 – 2 timar
Par

Å bevise Pytagoras’ setning

Å bevise Pytagoras setning

Emne

Dynamisk geometri, rettvinklet trekant, Pytagoras’ setning, bevis

Hensikt

Elevene skal lage et algebraisk bevis for Pytagoras’ setningen.+

Valg av tidspunkt

Mens elevene arbeider med Pytagoras’ setning eller algebra, eller som repetisjon.

Du trenger

PC med GeoGebra

Aktiviteten

Oppgave til elevene 

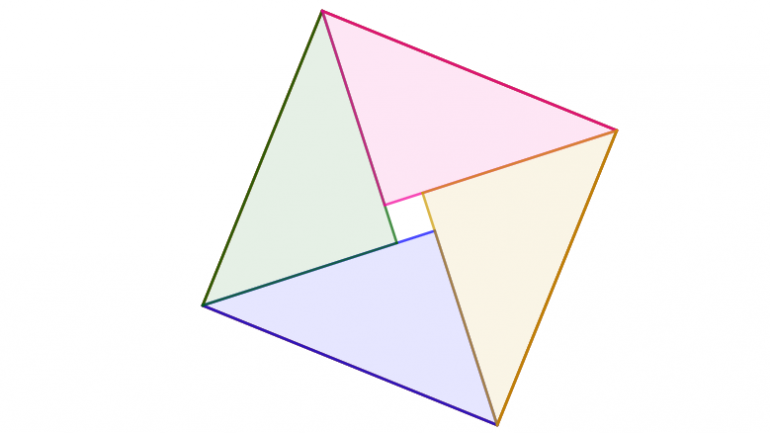
  • Åpne GeoGebra-filen https://www.geogebra.org/m/abyh23q8
  • Utforsk figuren og forklar oppdagelsene for hverandre.
  • Lag en skisse av figuren. Gi navn til sidene i trekanten. Like lange sider skal ha samme navn.
  • Finn ulike måter å beskrive arealet til det store kvadratet på.
  • Bruk dette til å bevise Pytagoras’ setning.

Kommentar til læreren

Elevene starter med å utforske en GeoGebra-figur. Noen vil gjenkjenne Tales’ setning og bruke det til å begrunne at trekantene er rettvinklet og at figuren i midten er et kvadrat. Tips gjerne elevene om at de kan åpne figuren i GeoGebra-appen (trykk på de tre punktene øverst til høyre). Da kan de undersøke mer, for eksempel om trekantene har like stort areal eller like store vinkler.

Ved å sammenligne arealer kan elevene bevise at Pytagoras’ setning stemmer. Elevene skal lage og sette navn på en skisse av figuren. På forhånd kan det være lurt å bli enige om navn, for eksempel at hypotenusen heter c, den lengste kateten heter a og den korteste kateten heter b. Det gjør det lettere å snakke om figuren og beviset i hel klasse.

Utfordre elevene til å finne ulike måter å skrive arealet til det store kvadratet på algebraisk. De fleste vil finne ut at de kan skrive arealet som c2­. Men elevene kan også bruke informasjonen de har om trekantene til å beskrive arealet.

Arealet til det store kvadratet = arealet til de fire (like) trekantene + arealet til «hullet»   
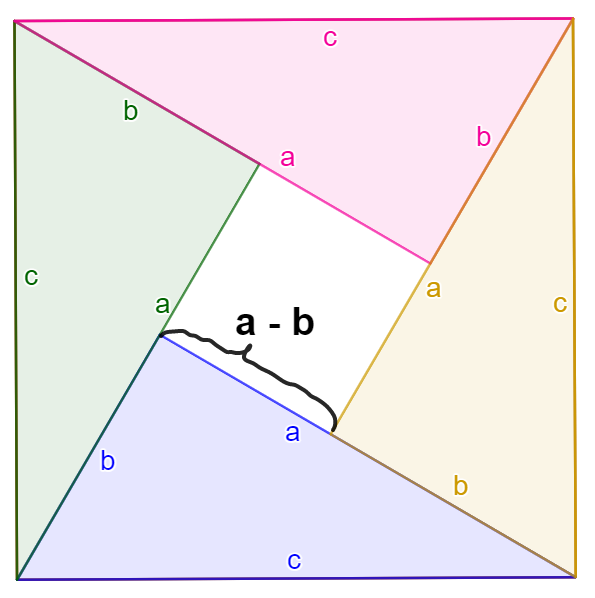
Figur med navn

`c^(2) = 4·(a · b)/(2) + HULL = 2ab + HULL`

Arealet til «hullet» kan by på utfordringer. De fleste vil oppdage at «hullet» er et kvadrat og da vet de at de kan regne ut arealet hvis de vet sidelengden. Selv om elevene har skrevet navn på alle sidene til alle trekantene, er det for mange utfordrende å komme fram til at kvadratsiden er a – b. Å finne et uttrykk for slike størrelser er viktig kunnskap i problemløsing. Noen elever vil ha nytte av å tenke at det er tallstørrelser som er oppgitt.

Arealet til hullet:

`(a - b)^(2) = a^(2) - 2ab + b^(2)`

Setter inn:
`c^(2) = 2ab + HULL`
`c^(2) = 2ab + a^(2) - 2ab + b^(2)`
`c^(2) = a^(2) + b^(2)`

Elevene blir ofte overrasket over at utregningen ender med Pytagoras’ setning.

Gode spørsmål

  • Hvorfor er de fire trekantene like store?
  • Hva trenger dere for å regne ut arealet til en rettvinklet trekant?
  • Beskriv med ord hva som er like stort som arealet til det store kvadratet.
  • Hvor lang er siden til det lille kvadratet?

Oppsummering

Gå gjennom og diskuter beviset i hel klasse. Tydeliggjør at beviset bygger på sammenligning av arealer med algebra som matematisk verktøy. Elevene kan også lage figuren selv i GeoGebra. Da er Tales’ setning og verktøyet Passer veldig nyttig. Ved å bruke Objekttekst kan de vise samme navn på flere objekter.