Algoritmisk tenking med GeoGebra 1
Emne
Lineær funksjon, stigningstall, konstantledd, midtpunkt, tyngdepunkt, tangent, derivert, algoritmisk tekning.
Hensikt
Elevene skal utvikle en økt forståelse av lineære funksjoner gjennom å bli kjent med de matematiske algoritmene som ligger bak noen av verktøyene i GeoGebra.
Valg av tidspunkt
Du trenger
PC og elevark.
Aktiviteten
Om prosjektet
Opplegget er utviklet av Freudenthal Institute, Utrecht University som del av prosjektet “Computational and Mathematical Thinking” (NRO, prosjektnummer 40.5.18540.130). Elevene skal bruke GeoGebra for å trene på algoritmisk tenking i arbeidet med rette linjer. Algoritmisk tenking handler om å dele opp en utfordring og løse hver del systematisk. Det er sentralt når elevene skal utvikle egne strategier og fremgangsmåter i matematikk.

Matematikksenteret har tilpasset undervisningsopplegget til norske forhold. Vi har valgt å dele inn undervisningsopplegget i to deler. I Algoritmisk tekning med GeoGebra 1 har Matematikksenteret valgt å dra nytte av samarbeidet vi har med Kikora. Oppgavene er tilpasset Kikora sin plattform slik at elevene får umiddelbar tilbakemelding underveis i arbeidet. I Algoritmisk tenking med GeoGebra 2 starter elevene arbeidet med blanke ark i GeoGebra. De må arbeide uten støtten fra de trinnvise instruksjonene i Kikora.
Undervisningsopplegget er en del av et internasjonalt prosjekt. Derfor ønsker vi tilbakemeldinger fra dere som bruker undervisningsopplegget med elever.
- Hvordan arbeidet elevene med oppgavene?
- Hvor lenge arbeidet de konsentrert?
- Hvilken aktivitet var mest utfordrende for elevene?
Send tilbakemeldinger til kontakt@matematikksenteret.no, merk med GeoGebra.
Introduksjon
I dette undervisningsopplegget skal elevene finne algoritmene som ligger bak verktøytastene i GeoGebra. Elevene skal først bruke et verktøy for å se hvordan det fungerer og deretter lage uttrykkene som gir ønsket resultat. Elevene arbeider på hver sin PC i par eller små grupper. De har hvert sitt elevark som de fyller ut underveis. Det er enklest for elevene å holde oversikten om de får elevarket på papir.
Mange av oppgavene tar utgangspunkt i formelen for lineære funksjoner, y = ax + b. Elevene må være kjent med hvordan de finner stigningstallet og konstantleddet når to punkter er gitt. For å finne stigningstallet bruker de x- og y-koordinatene. For å finne konstantleddet bruker de stigningstallet og koordinatene til et punkt som ligger på linjen. Elevene må også kjenne skrivemåten x(A) som gir x-koordinaten til punkt A og tilsvarende. Det kan de lære om i Lær GeoGebra: Funksjoner 2.
I de tre første oppgaverekkene bruker elevene skrivemåten for linjer, y = ax + b og ikke funksjoner f(x) = ax + b. Årsaken er at det fungerer bedre i GeoGebra. For en del elever vil det også være lettere å se sammenhengen mellom punkter og uttrykk med denne skrivemåten. For å skille linjene fra hverandre, må elevene gi dem navn, g: y = ax + b. Skrivemåten blir forklart, men minn de om det ved behov. I oppgaverekke 4 bruker elevene skrivemåten for funksjoner.
Hvis elevene har mange objekter av en type, kan Algebrafeltet bli uoversiktlig. Da kan de krympe en objekttype ved å trykke på streken foran navnet på objekttypen. Det er nyttig når elevene ikke trenger å se alle objektene i Algebrafeltet, men fungerer bare når objektene er sortert etter objekttype.
De fleste oppgavene slutter med at elevene skal bevege figuren. Ved å utnytte de dynamiske mulighetene i GeoGebra, kan elevene avgjøre om det de har gjort gjelder alltid, noen ganger eller aldri.
Aktivitet 1: Linje gjennom to punkter
Elevene skal gjøre oppgaverekke 1 i Kikora (oppgave 1.1 – 1.4). Målet med oppgavene er at elevene skal finne uttrykket for en linje gjennom to vilkårlige punkt.
I den første oppgaven er alle verktøy tilgjengelige. Elevene noterer uttrykket til linjen på elevarket. Det er dette uttrykket elevene vil komme fram til når de regner ut stigningstallet og konstantleddet med tallverdiene til x- og y-koordinatene.
Elevene vil oppdage at punkter og linje henger sammen om de bruker x(A), y(A), x(B) og y(B). Men når punktene A og B har samme x-koordinat, forsvinner linjen. For å unngå dette, må elevene bruke GeoGebra-kommandoer som minner om programmering. Kommandoen Dersom( <Vilkår>, <Så>, <Ellers> ) sørger for at linjen alltid er synlig. Elevene vil også ha bruk for kommandoen senere i opplegget.
Kommentar til læreren
Innholdet i disse oppgavene er sentralt i arbeidet videre så bruk god tid. Elevene skal bruke x(A), y(A), x(B) og y(B) i uttrykkene sine for å få objektene til å henge sammen. Notasjonen x(A) betyr at GeoGebra skal bruke verdien til x-koordinaten til punkt A. Hvis elevene beveger på punkt A, bruker GeoGebra den nye verdien. Tilsvarende for y(A), x(B) og y(B). Denne notasjonen er nyttig i dette opplegget og i mange andre sammenhenger. Legg vekt på at i kommandoen Dersom( <Vilkår>, <Så>, <Ellers> ) skriver elevene unntaket først og det generelle til slutt.
Det er ikke alle elever som forstår hvorfor linjen blir borte når A og B har samme x-koordinat. Be elevene om å sjekke uttrykket for stigningstallet. De vi se at nevneren blir null når x(A) og x(B) har samme verdi.
Noen spørsmål som kan hjelpe elevene videre:
- Hva kjennetegner en rett linje?
- Hvor finner du konstantleddet i uttrykket til linjen?
- Hvor finner du stigningstallet i uttrykket til linjen?
- Hvor finner du konstantleddet på grafen?
- Hvor finner du stigningstallet på grafen?
Aktivitet 2: Midtnormal
Elevene skal gjøre oppgaverekke 2 i Kikora (2.1 – 2.4). Målet med oppgavene er at elevene skal lage en midtnormal uten å bruke verktøyet eller den innebygde kommandoen Midtnormal.
I første oppgave bruker elevene Midtnormal for å se hva målet med oppgaverekken er. Formelen for å finne midtpunktet til et linjestykke står på elevarket. Elevene må forklare hvorfor formelen er riktig.
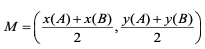
Også denne oppgaverekken slutter med en Dersom(<Vilkår>, <Så>, <Ellers>) kommando. Kommandoen er nødvendig for å tegne midtnormalen når linjestykket AB er horisontalt.
Kommentar til læreren
I den første oppgaven skal elevene bruke verktøy eller kommando for å finne midtpunktet og midtnormalen. Dersom de prøver å gjøre det samme i de neste oppgavene, vil de ikke få godkjent i Kikora. Elevene må skrive inn matematiske uttrykk.
Noen elever vil trenge hjelp til å finne stigningstallet til midtnormalen. Be elevene om å tegne noen linjer med kjent stigningstall i GeoGebra. Tegn en normal på hver linje og sammenlign stigningstallet til de to linjene. Elevene vil oppdage at hvis stigningstallet til en linje er a, så er stigningstallet til normalen til linjen `(- 1)/(a)`.
Noen spørsmål som kan hjelpe elevene videre:
- Hvordan finner du midtpunktet til en horisontal linje?
- Hvordan finner du midtpunktet til en vertikal linje?
- Hva ser du når du sammenligner stigningstallet til linjestykket og midtnormalen?
- Hvorfor blir midtnormalen borte når A og B har samme x-koordinat?
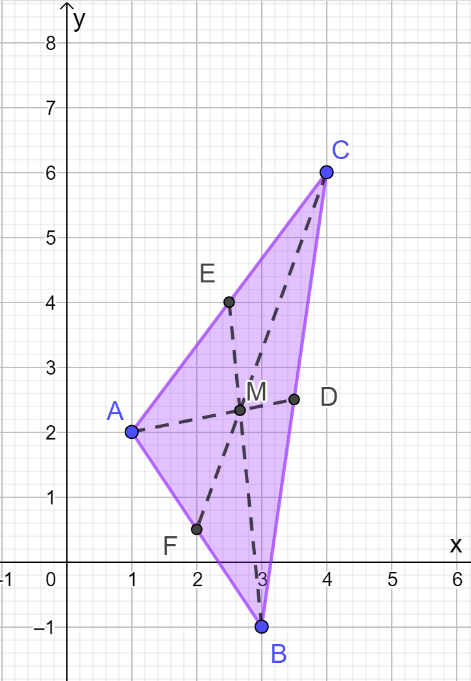
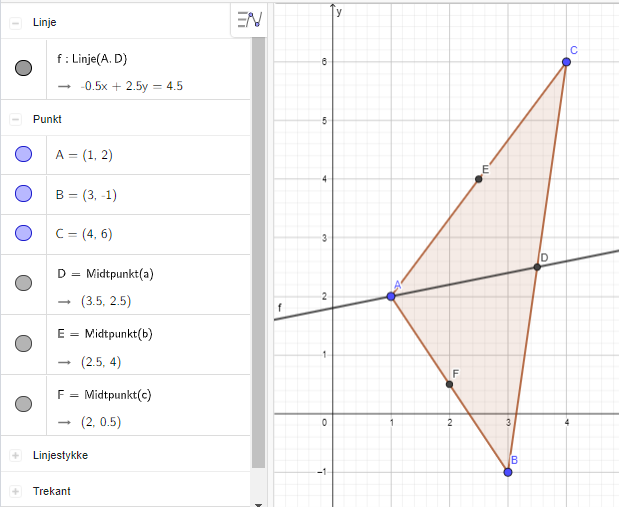
Aktivitet 3: Tyngdepunktet i en trekant
Elevene skal gjøre oppgaverekke 3 i Kikora (3.1 – 3.6). Målet er å finne tyngdepunktet til trekanten. Tyngdepunktet er punktet der medianene skjærer hverandre. En median går fra et hjørne til midtpunktet på den motstående siden.
I første oppgavene skal elevene bruke Midtpunkt eller sentrum for å finne tyngdepunktet til trekanten. Elevene noterer koordinatene til punktet. I de neste oppgavene skal de lære å finne tyngdepunktet uten å bruke verktøyet. Elevene starter med å finne midtpunktet til sidene. Deretter lager de uttrykket for linjen gjennom et hjørne og midtpunktet på motstående side, slik som de gjorde i første oppgaverekke.
Kommentar til læreren
På elevarket er det laget en tegning av trekanten som elevene kan bruke som skisse. Ved å bruke den blir det enklere til å ha kontroll over alle punkter og linjer. Elevene får lov til å bruke den innebygde kommandoen Skjæring for å finne tyngdepunktet. Elever som trenger ekstra utfordringer, kan å finne skjæringspunktet med CAS.
GeoGebra gir alle objekter navn automatisk. I oppgave 3.2 er det derfor lurt at elevene lager midtpunktene i samme rekkefølge som står på i oppgaven (og på elevarket), slik at punktene får riktig navn med en gang.
Noen oppgaver er delt i to i Kikora slik at det ikke skal være for mange steg. Da starter den andre oppgaven med resultatet av det elevene har gjort i den første oppgaven.
Aktivitet 4: Tangenten til parabler
Elevene skal gjøre oppgaverekke 4 i Kikora (4.1 – 4.4). Målet er at elevene skal bli bedre kjent med ettpunktsformelen. På forhånd må de vite at den deriverte i et punkt er det samme som stigningstallet til tangenten i punktet.
Elevene arbeider med funksjoner. I første oppgave oppdager elevene hvordan formelen f(x) = a(x - x1) + y1 fungerer. Resten av oppgaverekken følger samme oppskrift som tidligere oppgaverekker. Først bruker elevene verktøy for å lage tangenten til en funksjon, og deretter skal de bruke uttrykk og kommandoer for å gjøre det samme.
Kommentar til læreren
Elevene skal bruke det de har lært om funksjoner og GeoGebra til å lage en dynamisk tegning som viser sammenhengen mellom tangent og funksjon. Notasjonene x(A) og f(x(A)) er sentrale. Ved å bruke disse skrivemåtene kan elevene lage dynamiske figurer, samtidig som de unngår slurvefeil som ofte kommer når de skal skrive inn lange uttrykk i GeoGebra.
I oppgave 4.4 skal elevene skrive A = (a, f(a)) for å lage et punkt på grafen til f. GeoGebra lager da en glider a som styrer punkt A.
Oppsummering
Det er mulig å oppsummere det faglige innholdet underveis, for eksempel etter en oppgaverekke, eller når elevene er ferdig med alle oppgavene. I oppsummeringen er det viktig å få fram verdien av algebra. Elevene er nødt til å bruke variabler for å gjøre figurene dynamiske. I tillegg gjør bruk av variabler det lettere for elevene å se sammenhenger.
Elevene har også sett litt bak verktøyene i GeoGebra. De har gjort seg erfaringer om hvordan de kan lage matematiske uttrykk som gir de resultatet de ønsker og hvordan de kan få objekter til å henge sammen. I tillegg har de erfart hvordan programmerere må tenke når de lager verktøy. For eksempel måtte de omdefinere uttrykket for linjen i oppgave 1.4 slik at den ikke forsvant når x-verdiene til punktene var like.
Algoritmisk tenking med GeoGebra 2 er en fortsettelse av dette undervisningsopplegget og elevene skal arbeide videre med tangenter. De starter med blanke ark i GeoGebra uten Kikora som støtte.
Rammeplanmål/Kompetansemål
- Videregående
- R1
- analysere og tolke ulike funksjoner ved å bruke derivasjon
- utforske, analysere og derivere ulike funksjoner og deres omvendte funksjoner, og gjøre rede for egenskaper til og sammenhenger mellom slike funksjoner
- R2
- analysere og tolke ulike funksjoner ved å bruke derivasjon og integrasjon, og anvende integrasjon til å beregne ulike mål av omdreiningslegemer
- S1
- uttrykke egne resonnementer ved hjelp av matematiske begreper og symbolspråk
- S2
- analysere og tolke ulike funksjoner ved å bruke derivasjon og integrasjon
- Vg1P
- bruke digitale verktøy i utforsking og problemløysing knytt til eigenskapar ved funksjonar, og diskutere løysingane
- identifisere variable storleikar i ulike situasjonar og bruke dei til utforsking og generalisering
- tolke og bruke funksjonar i matematisk modellering og problemløysing
- Vg1T
- formulere og løyse problem ved hjelp av algoritmisk tenking, ulike problemløysingsstrategiar, digitale verktøy og programmering
- identifisere variable storleikar i ulike situasjonar, setje opp formlar og utforske desse ved hjelp av digitale verktøy