Andregradsfunksjoner 5
Opplegget er en revidert versjon fra heftet Undersøkende matematikkundervisning i videregående skole.
Emne
Andregradsfunksjon, funksjonsuttrykk, nullpunkt, faktor, faktorisert form
Hensikt
Elevene skal oppdage og generalisere sammenhengen mellom andregradsfunksjoner på formen f(x) = ax2 + bx + c og på faktorisert form.
Valg av tidspunkt
Du trenger
PC med GeoGebra og elevark.
Aktiviteten
Elevene arbeider med andregradsfunksjoner hvor funksjonsuttrykket er oppgitt på formen f(x) = ax2 + bx + c og på faktorisert form. La elevene oppdage sammenhengene selv, og oppfordre dem til å diskutere underveis og til å bruke matematiske ord og uttrykk. Bruk helklassesamtaler for å løfte fram oppdagelser.
Aktivitet 1
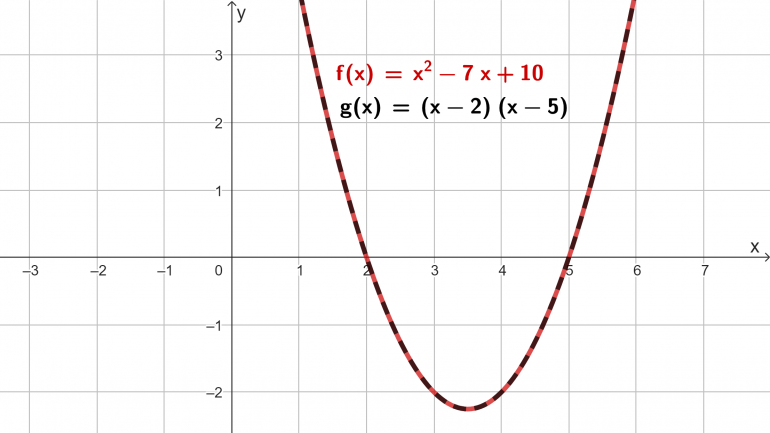
Klassen gjør første aktivitet sammen. Læreren tegner grafene til f(x) = x2 - 7x + 10 og g(x) = (x - 2)(x - 5) i GeoGebra og klassen studerer grafene. Målet er at elevene skal oppdage at andregradsuttrykkene gir den samme grafen.
Kommentar til læreren
Gode spørsmål:
- Hva oppdager dere? Hvorfor er det slik?
- Hva slags funksjoner er f og g?
- Hva er nullpunktene til funksjonene?
- Vi sier at funksjonen g er skrevet på faktorisert form. Hvorfor?
I tillegg til å snakke om spørsmålene nevnt over, er det viktig at elevene forstår hva faktorisert form betyr og hva som er fordelen med den.
På elevarket er det satt av plass til at elevene kan oppsummere helklasseaktiviteten med egne ord.
Aktivitet 2
Elevene arbeider med aktivitet 2 på elevarket. Utgangspunktet er funksjonsuttrykk gitt på faktorisert form, og elevene skal finne nullpunktene og funksjonsuttrykk på formen f(x) = ax2 + bx + c. Målet er at de skal generalisere sammenhengen mellom uttrykkene.
Kommentar til læreren
Hvis klassen har gjennomført opplegget Andregradsfunksjoner 4, er sammenhengen mellom andregradsfunksjon på faktorisert form og dens nullpunkter kjent. Nå skal de lage et generelt uttrykk som beskriver sammenhengen mellom faktorisert form og formen f(x) = ax2 + bx + c. På elevarket skal elevene først se på noen konkrete eksempler og deretter prøve å lage et generelt uttrykk som viser sammenhengen med a, b og c. Siden alle uttrykkene består av to parenteser med kun én x i hver, vil a = 1 for alle uttrykkene. Ved å multiplisere sammen parentesene i k(x) = (x + s)(x + t) og samle ledd av samme grad, kan elevene komme fram til at k(x) = x2 + (s + t) x + (s ∙ t). Altså er b = s + t og c = s ∙ t.
Aktivitet 3
Elevene tar utgangspunkt i funksjonsuttrykk på formen f(x) = ax2 + bx + c. Målet er å bruke sammenhengen fra aktivitet 2 for å omskrive uttrykkene til faktorisert form.
Kommentar til læreren
Å kunne skrive funksjonsuttrykket til andregradsfunksjoner om til faktorisert form er en nyttig metode for å finne nullpunktene til funksjonen på. Det er også kjekt hvis brøker eller brøkfunksjoner inneholder andregradsuttrykk.
Aktivitet 4
Elevene undersøker andregradsfunksjoner hvor a ≠ 1. Målet er å utvikle metoden fra aktivitet 2 og 3 til å gjelde for alle andregradsfunksjoner.
Kommentar til læreren
De starter med å sammenligne en andregradsfunksjon hvor a = 1 med en funksjon hvor alle ledd er doblet. Funksjonene har like nullpunkter og forskjellig krumning. Mange elever synes det er vanskelig å beskrive matematikk med egne ord. Spørsmålene «Hva er forskjellig?» og «Hva er likt?» kan hjelpe elevene i gang.
Forslag til regel for å faktorisere:
Hvis x = s og x = t er nullpunktene til en andregradsfunksjon, f(x) = ax2 + bx + c, kan f faktoriseres slik: f(x) = a(x - s)(x - t).
Oppsummering
Avslutt med en helklassesamtale. Løft fram matematiske ord og uttrykk som elevene bruker.
Gode spørsmål:
- Hva er fordelen med faktoriserte uttrykk?
- Hva er sammenhengen mellom faktorisert form og nullpunkter?
- Hva er sammenhengen mellom faktorisert form og a-b-c-form?
- Har alle andregradsfunksjoner en faktorisert form? Hvorfor/hvorfor ikke?
Rammeplanmål/Kompetansemål
- Videregående
- Vg1P
- bruke digitale verktøy i utforsking og problemløysing knytt til eigenskapar ved funksjonar, og diskutere løysingane
- identifisere variable storleikar i ulike situasjonar og bruke dei til utforsking og generalisering
- tolke og bruke formlar som gjeld samfunnsliv og arbeidsliv
- Vg1T
- formulere og løyse problem ved hjelp av algoritmisk tenking, ulike problemløysingsstrategiar, digitale verktøy og programmering
- identifisere variable storleikar i ulike situasjonar, setje opp formlar og utforske desse ved hjelp av digitale verktøy
- utforske og beskrive eigenskapane ved polynomfunksjonar, rasjonale funksjonar, eksponentialfunksjonar og potensfunksjonar
- utforske samanhengar mellom andregradslikningar og andregradsulikskapar, andregradsfunksjonar og kvadratsetningane og bruke samanhengane i problemløysing
