Areal av trekanter - geometriske steder

Emne
Ulike trekanter med likt areal. Konstruksjon med passer og linjal.
Hensikt
Elevene skal få erfaring med og forståelse for geometriske steder ved å bruke kunnskaper om areal av trekanter. De skal øve seg på å skrive en matematisk tekst med bruk av illustrasjoner, riktige begreper, resonnement og bevis.
Valg av tidspunkt
Du trenger
Passer og linjal.
Blanke ark.
Aktiviteten
Arbeidsform:
Smågrupper med to til tre elever. La elevene dele og diskutere i plenum. Til slutt skal de skrive en matematisk tekst om det de har funnet ut.
Undervisningsopplegget:
Elevene skal starte med å tegne en trekant midt på arket. De bestemmer selv formen på trekanten. Den skal ikke være for stor. Elevene skal først lage skisser og forklare løsningene sine. Deretter skal de konstruere med passer og linjal.
Oppgave:
- Tegn en trekant midt på arket.
- Lag minst to trekanter med samme areal som den du har tegnet. Trekantene skal ha én side felles med den trekanten du startet med. (Elevene skal gjøre denne oppgaven individuelt.)
- Sammenlikne løsningene dine med løsningene til de andre på gruppa. Diskutér hva som må være oppfylt for at trekanter med en felles side skal ha samme areal.
- Finnes det flere trekanter med samme areal? Diskutér på gruppa: Hvor må toppunktene ligge? Lag skisser. Forklar og begrunn løsningene deres.
- Tegn en ny trekant. Konstruer løsningene på oppgaven med passer og linjal.
- Dere har funnet det geometriske stedet for toppunktet til trekanter med samme areal og en felles side med en gitt trekant. Forklar hva som menes med et geometrisk sted, og hvorfor dette er «et geometrisk sted» (Kan sløyfes for 1T og ungdomstrinnet).
- Lag en matematisk tekst med illustrasjoner, forklaringer og bevis på det dere har funnet ut.
Kommentarer til læreren:
La elevene utforske oppgaven. Bruk god tid. Kanskje noen elever kommer med helt spesielle løsninger, som rettvinklede trekanter eller likebeinte trekanter. Det bør komme fram i diskusjonen at det finnes uendelig mange løsninger. Hør på elevenes diskusjoner, og få ulike forslag fram i fellesdiskusjon på slutten av økta. Du kan vurdere om du vil la elevene lage den matematiske teksten før dere tar plenumsdiskusjonen. Da kan du se på de ulike løsningene, og velge ut noen som skal få presentere løsningene sine for klassen/gruppa.
Oppsummering og løsningsforslag:
Få fram elevenes tanker og hvordan de nærmet seg løsningene, ikke bare det endelige resultatet.
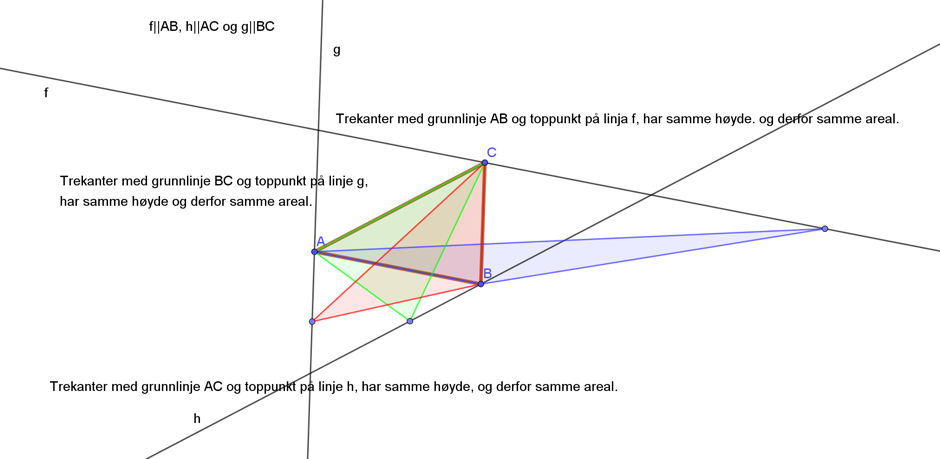
Forslag til videre arbeid:
Arbeid videre med geometriske steder. Se undervisningsopplegget «Geometriske steder/geometriske sammenhenger»
Rammeplanmål/Kompetansemål
- Videregående
- Vg1P
- utforske korleis ulike premissar vil kunne påverke korleis matematiske problem frå samfunnsliv og arbeidsliv blir løyste
- Vg1T
- modellere situasjonar knytte til ulike tema, drøftedrøfte, presentere og forklare resultata og argumentere for om modellane er gyldige
- Vg2P
- utforske og forklare korleis formlikskap, målestokk og eigenskapar ved geometriske figurar kan brukast i berekningar og i praktisk arbeid
- Grunnskole
- Kompetansemål etter 9.trinn
- utforske eigenskapane ved ulike polygonar og forklare omgrepa formlikskap og kongruens
- utforske og argumentere for korleis det å endre føresetnader i geometriske problemstillingar påverkar løysingar
