Eksponentialfunksjoner og papirbretting

Emne
Eksponentialfunksjoner, matematisk modellering og papirbretting.
Utviklet ved Molde videregående skole
Hensikt
Elevene bretter papir, beregner tykkelsen på det brettede papiret og arealet. Ved å starte praktisk skal elevene komme fram til en modell for tykkelsen av en papirbunken og arealet etter n brettinger.
Du trenger
Ett A3-ark per gruppe, en bunke med 500 A4-ark i samme tykkelse, linjal.
Aktiviteten
Areal
- Start med et A3-ark, mål hver av sidene og beregn arealet.
- Brett arket nøyaktig i to en gang, mål eller beregn sidene og arealet. Gjenta brettingen, og mål eller beregn hver gang sidene og arealet. Hvor mange brett klarer du? Fyll ut tabellen.
Antall brett
0
1
2
3
4
5
6
lengde
bredde
areal
- Lag en matematisk modell som kan brukes til å finne arealet etter x brettinger.
|
A(x)= |
Tykkelse
- Beregn tykkelsen på et ark ved å måle tykkelsen av det sammenbrettede godt sammentrykte papiret etter 6 brett. Alternativt kan en måle tykkelsen av en bunke som inneholder 500 ark.
Tykkelsen av et ark:
- Når du bretter arket vil antall lag med papir og dermed tykkelsen på det brettede papiret øke. Fyll ut tabellen under.
Antall brett
0
1
2
3
4
5
6
Antall lag med papir
Tykkelse (mm)
- Framstill resultatene i tabellen grafisk.
- Finn en matematisk modell, T(x), for tykkelsen av papirene.
T(x)=
- Rent teoretisk: Hvor mange ganger måtte du ha brettet hvis tykkelsen skulle passere 1 meter?
- Avstanden fra jorda til månen er ca 380 000 km. Rent teoretisk: Hvor mange ganger måtte vi brette hvis tykkelsen skulle bli like høy som avstanden fra jorda til månen?
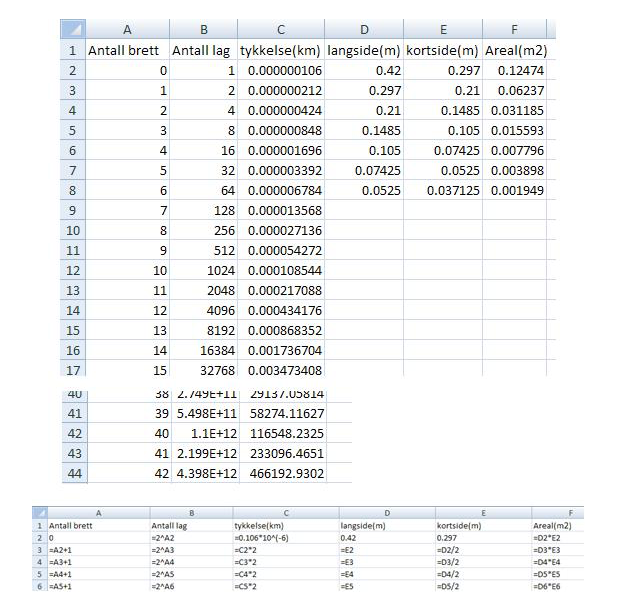
Eksempel på verdier: Arktykkelsen kan være (53:500)mm=0,106 mm
Modellen for tykkelsen blir for eksempel T(x) = 0.106 · 2x
Oppgaven er godt egnet til å jobbe med i regneark.
Rammeplanmål/Kompetansemål
- Videregående
- R1
- modellere og analysere eksponentiell og logistisk vekst i reelle datasett
- R2
- gi eksempler på ulike situasjoner som kan modelleres ved å bruke ulike matematiske funksjoner, og modellere og analysere slike situasjoner ved å bruke reelle datasett
- S2
- modellere og analysere eksponentiell og logistisk vekst i reelle datasett
- Vg1P
- tolke og bruke funksjonar i matematisk modellering og problemløysing
- bruke digitale verktøy i utforsking og problemløysing knytt til eigenskapar ved funksjonar, og diskutere løysingane
- Vg1T
- utforske og beskrive eigenskapane ved polynomfunksjonar, rasjonale funksjonar, eksponentialfunksjonar og potensfunksjonar
- Grunnskole
- Kompetansemål etter 10. trinn
- utforske og samanlikne eigenskapar ved ulike funksjonar ved å bruke digitale verktøy
- utforske samanhengen mellom konstant prosentvis endring, vekstfaktor og eksponentialfunksjonar
