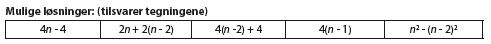Figurtall, følger og rekker - Ramme

Emne
Mønster og sammenhenger.
Dette opplegget er hentet fra heftet Undersøkende matematikkundervisning i videregående skole II.
Hensikt
LÆRINGSMÅL
- Eleven skal gjennom praktisk arbeid finne mønster og sammenhenger.
- Eleven skal finne både rekursiv og implisitt formel for mønster.
- Eleven skal finne sammenhenger mellom forskjellige representasjoner.
- Eleven skal vise at algebraiske uttrykk er like.
- Eleven skal anvende algebra i praktiske sammenhenger.
- Eleven skal bruke digitale hjelpemidler til å finne og/eller bekrefte svaret.
- Eleven skal finne kjennetegn for aritmetiske og geometriske rekker.
Eleven skal beregne summen og grenseverdier av aritmetiske og geometriske rekker.
Felles for disse oppleggene er at elevene skal finne frem til et matematisk uttrykk. De fleste starter med at elevene bygger figurer. Elevene vil besvare oppgavene på forskjellige måter. Av den grunn er det viktig at man fører en klassesamtale i etterkant der de ulike strategiene og løsningene blir sammenlignet.
Du trenger
Firkantede tellebrikker
Aktiviteten
Opplegget har tre aktiviteter, hver av dem med utgangspunkt i oppgaver som læreren gir elevene muntlig.
AKTIVITET 1
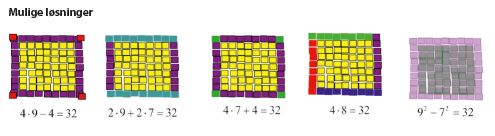
• Tenk deg et kvadrat laget av 81 kvadratiske brikker. De ytterste brikkene i kvadratet kaller vi rammen. Hvor mange brikker er det i rammen?
Kommentar til læreren
Svaret 32 noteres på tavlen. Selve svaret er uinteressant, for i dette opplegget er det viktigere å fokusere på de ulike strategiene elevene bruker. Læreren skal notere alle de ulike fremgangsmåtene elevene har brukt for å komme frem til 32.
AKTIVITET 2
• Tegn eller legg en figur som viser hvordan du har tenkt.
• Tegn eller legg figurer som viser andres tenkemåter.
Kommentar til læreren
Elevene blir først utfordret til å visualisere sin egen løsning ved å tegne den eller legge den med brikker. Etterpå skal de sette seg inn i løsninger som andre elever har presentert og tegne disse løsningene.
AKTIVITET 3
• Alle figurene som er laget hittil, kaller vi for figur 9, da sidene er 9 brikker lange.
• Hvis det var n brikker langs siden, hvor mange brikker trenger man da til rammen? Start med å lage eller tegne figur 4, 5 og 6.
Kommentar til læreren
Før utvidelsen til n bør elevene begynne med mindre kvadrater. Det går raskere og det er lettere å beholde oversikten dersom man legger få brikker. Derfor oppfordres elevene til å starte med et kvadrat med sidelengde 4, så et med sidelengde 5, for så å fortsette med sidelengde 6 osv. Det er en fordel at elevene samler resultatene i en tabell der de ikke bare noterer svaret, men også regnestykket som ligger bak. Da er det lettere å se hva som endrer seg og hva som forblir likt.
Overgangen fra tall til variabel er vanskelig for mange elever, og det er viktig at disse elevene får nok tid. Andre elever vil derimot finne formelen for n direkte ut fra samtalen i den første oppgaven. Hvis forklaringene er tydelige og tegningene er gode, er det bare å erstatte 9 med n. Disse elevene trenger selvsagt ikke å lage mange kvadrater, men trenger nye utfordringer. Se utvidelsen av oppgaven.
Læreren må ta seg tid til å vise at alle tenkemåtene er riktige, og at alle formlene gir det samme svaret. Det er viktig å vise at alle svarene er riktige ved å omforme dem algebraisk.
UTVIDELSE AV OPPGAVEN
Elevene oppfordres til å legge et rektangel og finne formler for rammen rundt figuren. Siden forholdet mellom sidene er valgfritt, vil denne oppgaven ha individuelle svar.
Rammeplanmål/Kompetansemål
- Videregående
- S1
- uttrykke egne resonnementer ved hjelp av matematiske begreper og symbolspråk
- Vg1P
- modellere situasjonar knytte til tema frå samfunnsliv og arbeidsliv, presentere og argumentere for resultata og for når modellane er gyldige
- identifisere variable storleikar i ulike situasjonar og bruke dei til utforsking og generalisering
- Vg1T
- identifisere variable storleikar i ulike situasjonar, setje opp formlar og utforske desse ved hjelp av digitale verktøy
- modellere situasjonar knytte til ulike tema, drøftedrøfte, presentere og forklare resultata og argumentere for om modellane er gyldige
- Vg2P
- utforske strategiar for å løyse likningar, likningssystem og ulikskapar og argumentere for tenkjemåtane sine