Fraktaler

Fraktaler, geometriske rekker, uendelighet

Fraktaler er matematiske objekter som ikke bare er vakre å se på, men som også skaper interesse og motivasjon hos elevene som jobber med dem. Å jobbe med fraktaler gir muligheter til å utvikle ideer fra blant annet algebra og geometri og se sammenheng mellom dem.

Papir og blyant,

I dette opplegget skal elevene først lage noen kjente fraktaler etter gitt beskrivelse. Etterpå skal de bruke fantasi og lage egne fraktaler. I begge tilfeller skal utforskning og diskusjon vektlegges. Sammenheng mellom egenskaper til fraktaler og geometriske rekker skal tydeligjøres.

På de neste sidene blir 3 aktiviteter presentert med kommentarer til læreren. 

Introduksjon av opplegget

Kommentar til læreren:
Introduser gjerne fraktaler som matematiske strukturer med den fantastiske egenskapen at når en fraktal brytes i små deler, er hver del en eksakt kopi av den opprinnelige formen.
Be elevene om å tenke på hvor rart det ville vært hvis de skulle slippe et glass vann i bakken og glasset ble knust i 100 biter, og hver av bitene ville vært et svært lite glass fylt med vann. Denne umulige idéen er nøyaktig hva som skjer med fraktaler.

Aktivitet 1 – Fraktaltre

Elevene skal lage et fraktaltre og fylle ut en tabell.

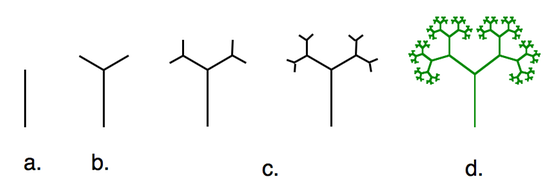
1. Tegn et fraktaltre ved å følge  punktene:

     a. Tegn en trestamme
     b. Tegn to greiner som kommer ut fra stammen, hver av dem halvparten så lang som stammen.
     c. Gjenta dette med to nye greine som kommer ut fra forrige greiner. Hver ny grein skal være halvparten så lang som greinene i forrige steg.
     d. Fortsett med dette til du kommer til "uendelig".  Din fraktal er fullført.

2. Fyll ut tabellen se kopieringsoriginal 

3. Hvilke mønster ser du? Beskriv dem.

4. Prøv å finne den algebraiske formelen for verdien i n-te trinn. Forklar hvordan du har kommet fram til svaret.

Kommentar til læreren:
La elevene arbeide seg gjennom punktene. Ha en diskusjon med elevene om hva de observerer. Hvis nødvendig, hjelp dem til å formulere den algebraiske formelen.

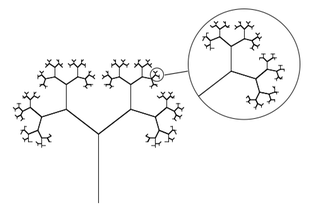
Forslag til noen konklusjoner:

• Hver del av treet er en eksakt kopi av hele treet. Man kan zoome inn og se den samme formen om og om igjen, eller man kan zoome ut. Kanskje treet vi har tegnet er bare en liten bit av et tre som er tusenvis km høy!
• Den totale lengde er uendelig, men grensen for lengden fra rota til ytterste grein er 2. Prøv å få elevene til å knytte tallet 2 til summen av uendelige geometriske rekker. `(1+ 1/2 + 1/4 + 1/8 +... = 2)`

Aktivitet 2 – Sierpinski-trekant

Sierpinski-trekanten er en av de mest interessante og vakreste fraktaler. Den er oppkalt etter Waclaw Sierpinski (1882-1969), en polsk matematiker som er kjent for sitt arbeid med blant annet fraktaler.

Elevene får en kopi av arket (kopieringsoriginal) og skal følge instruksjoner.
Underveis skal de også fylle ut tabellen.

Oppgave:

1. Finn midtpunktet på hver av sidene i trekanten.
2. Koble midtpunktene til hverandre med rette linjer.
3. Nå har du 4 like store trekanter i den store trekanten. Den midterste trekanten fargelegger/skyggelegger du med svak gråtone for å representere at den miderste trekant har blitt tatt bort. 
4. Gjenta trinn 2 for de tre gjenværende trekanter, det vil si finn midtpunktene av hver av sidene i hver av trekanter og koble dem.

Gjenta det samme på de 9 gjenværende trekanter, og fortsett til trekantene er for små til å tegne videre.

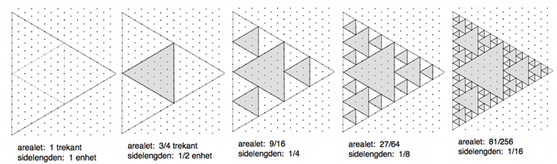
Spørsmål:

• Hvordan endrer sidelengden seg for hvert trinn? Hva skjer når vi går mot uendelig?

• Hvordan endrer arealet seg? Hva skjer når vi går mot uendelig?

Aktivitet 3

Kunst med fraktaler

La elevene eksperimentere med å skape sine egne fraktaler.

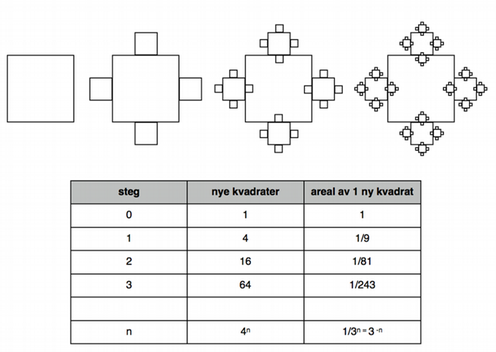
1. Velg en figur (for eksempel en kvadrat eller trekant) og bestem en ‘regel’ (framgangsmåte) som skal følges for å lage en fraktal du ønsker
2. Bruk regelen på figuren du har valgt i punkt 1
3. Gjenta punkt 2 mange ganger

En god regel må resultere i minst to mindre kopier av utgangsfiguren, slik at den kan gjentas på de mindre kopiene. En regel kan innebære å legge til eller trekke fra deler av figuren, ved hjelp av andre former eller ved hjelp av farger. Du bør være i stand til å zoome inn på figuren din, og fortsatt kunne se kopier av utgangsfiguren.

     4. Lag en tabell som viser hvordan en eller flere egenskaper av fratalen endrer seg fra steg til steg. Egenskaper kan være antall nye former på hvert steg, størrelse av formene (lengden, arealet eller volumet), totalt antall former, osv.

Kommentar til læreren:

La elevene bruke kreativitet. Du kan vise eksemplene under. 

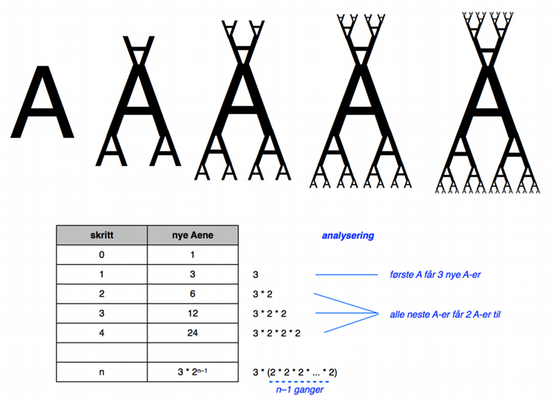
Elevene kan for eksempel bruke første bokstaven i navnet sitt. I denne "A-fraktalen" legger vi i første steg til 3 A-er, og i de neste stegene legger vi bare 2 A-er til hver A. Se på tabellen og analysen under. Det kan være veldig nyttig å skrive antall deler som et produkt for å lettere se hvordan vi kan skrive en formel for det n-te steget.

Elever kan fritt velge farger og former. Sirkelfraktalen under innholder potens med 2, og blomsterfraktalen innholder potens med 3.