Fullstendig kvadrat

Faktorisering, algebra, matematiske begreper.

Elevark 1 og elevark 2

Innledning

I lærebøkene som blir brukt i den videregående opplæringen blir fullstendig kvadrat presentert på følgende måte.

• Et fullstendig kvadrat er et andregradsuttrykk som vi kan faktorisere ved hjelp av den første eller den andre kvadratsetningen. (Sinus 1T)
• I de tilfelle vi kan faktorisere et uttrykk ved å bruke første eller andre kvadratsetning baklengs, har vi det vi kaller et fullstendig kvadrat (Matematikk 1T)
• Du skal lære
  • Regelen for å bygge opp et fullstendig kvadrat ved å halvere, kvadrere og addere
  • Å bruke et fullstendig kvadrat til å finne største eller minste verdi av andregradsuttrykk (Sigma 1T)

Alle beskrivelser for fullstendig kvadrat inneholder mange matematiske begreper. Men ingen av de tre bøkene gir en forklaring for navnet «fullstendig kvadrat». To av bøkene nevner at det er en måte å faktorisere, den tredje nevner først en huskeregel og så en mulig anvendelse.

Målet med dette undervisningsopplegget er at elevene skal få en dypere forståelse for uttrykket «fullstendig kvadrat» å visualisere problemet.

Opplegget tar utgangspunkt i en litt endret forklaring fra Sinus 1T.

Aktivitet 1

Elevene jobber i par med elevark 1. Paret må diskutere med hverandre for å bli enige om forklaringen de skal skrive ned.

Et fullstendig kvadrat er et andregradsuttrykk som vi kan faktorisere ved hjelp av den første eller den andre kvadratsetningen.

• Finn de matematiske begrepene i setningen, noter dem i boksen og skriv en forklaring.

Avslutt denne sekvensen med en oppsummerende klassesamtale.

Kommentar til læreren

Setningen inneholder veldig mange matematiske begreper. Noen begreper er så kjent at elevene ikke vil oppfatte dem som «matematiske begreper» for eksempel «kvadrat», mens andre som «andregradspolynom» virker ukjent. Det er viktig å presisere at elevene skal bruke egne ord for å skrive en forklaring. Det er ikke lov å åpne boka eller internett.

Når læreren oppsummerer kan hun gjerne komme med gode spørsmål som:

• Hvorfor heter det kvadratsetning?
• Hva menes med faktorisering
• Når bruker vi faktorisering:
  • Forkorte brøk
  • Finne nullpunkter
  • Jobbe med andregradsuttrykk

Begrepet «fullstendig kvadrat» er læringsmålet av denne økta og blir ikke forklart ennå.

Aktivitet 2

Elevene jobber i par med elevark 2.

1. Skriv arealet av dette rektangelet som et algebraisk uttrykk på så mange måter som mulig
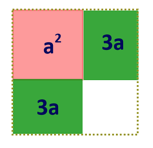
2. Her er to nye figurer. De er en fortsettelse av figur 1
3. Hvorfor er alle uttrykkene nedenfor lik a² + 6a
4. Se på det siste uttrykket. Sammenlign dette uttrykket med a² + 6a. Hva er forskjellen mellom uttrykkene?
5. «Halvere – kvadrere – addere og subtrahere» er en huskeregel for faktorisering med fullstendig kvadrat.
   
   Forklar hvordan denne huskeregelen passer til det som du har gjort.

Avslutt aktiviteten med en klassesamtale. Legg vekt på at alle elevene kan presentere noen av sine løsninger, selv om de ikke har kommet helt i mål.

Kommentar til læreren

Med hjelp av elevark 2 får elevene en visuell tilgang til begrepet «fullstendig kvadrat». Det skal så føre til en dypere forståelse for begrepet. Allerede figur 1 kan gi utfordringer. Mange elever er uvant ved å tegne. Dybdelæring krever flere tilnærmingsmåter.

I oppgave 1 forventer vi svar som: a² + 6a, eller a · a + 6 · a, eller a (a + 6). Hvis noen elever svarer for eksempel 6 a³ eller 6a², må disse misforståelser rettes opp med en gang, da alt arbeid er avhengig av at eleven kan reglene for enkel algebra.

Mens eleven jobber videre med oppgavene skal læreren gå rundt og lytte til samtalene elevene imellom.Misforståelser og mangelfull forståelse kan bli avdekket på denne måten. Ikke forstyrr elevene, men ta notater som du tar fram i den oppsummerende samtalen. Mange elever vil ha vanskeligheter ved å se og forstå bruken konjugatsetningen.( oppgave 3)

Legg spesiell vekt på at vi har faktorisert uttrykket, som er målet for aktiviteten. Forklar gjerne en gang til hva som skiller et faktorisert uttrykk fra et utrykk bestående av mange ledd og hva som er fordelen med faktorer i forhold til ledd. (oppgave 4)

Hvis noen elever er veldig fort ferdig med oppgaven, og du mener at resten av klassen skal få litt mer tid, kan du be dem å løse en ligning der de kan bruke denne metoden. Her er det vist et eksempel hvordan man kan løse en ligning med hjelp av fullstendig kvadraters metode.

Aktivitet 3 (tilleggsoppgave)

• Løs likningen a² + 6a = 11.
• Legg merke til at den venstre siden av ligningen er lik som uttrykket i elevark 2.
• Bruk huskeregelen for å løse ligningen. Forklar hva som skjer ved de enkelte skritt. «Halvere – kvadrere – addere og subtrahere»

Kommentar til læreren

Denne oppgaven kan gis muntlig eller på små lapper. Dette er et forslag til løsning med kommentar:

Å bruke fullstendig kvadrat er ikke den meste effektive metoden for å løse en andregradslikning. Derimot vil det å skrive en andregradsfunksjon faktorisert til fullstendig kvadrat gi ny informasjon om funksjoner og så føre til en bedre forståelse.