Hundrekartet - mønster og bevis

Tallmønster, rekursiv og eksplisitt formel

Dette opplegget er hentet fra heftet: "Undersøkende matematikk - undervisning i videregående skole"

Hundrekart og tellebrikker

Kopieringsorginal av hundrekartet

Undervisningsopplegget:

La elevene arbeide parvis. Det er viktig å oppmuntre til samtale og diskusjon om faglig arbeid. elevene skal skrive ned det de oppdager, både med ord og matematiske symboler.

Denne oppgaven er åpen i den forstand at det ikke er formulert spørsmål hvor elevene skal finne de riktige svarene. Det er et opplegg hvor elevene skal arbeide med utforskning.



Utgangspunktet er hundrekart og plastbrikker, og matematikken må tas i bruk som et verktøy for å observere, eksperimentere, gjette på systemer, prøve ut og verifisere eller forkaste gjetningen. De må analysere, systematisere og generalisere. De inviteres også selv til å formulere nye problemstillinger med utgangspunkt i systemet de forsker på. og til slutt kreves at de skal bevise at systemene de har funnet, er allmenngyldige.

I slike utforskningsoppgaver får elevene erfaring i å tenke matematisk. Vi ønsker at de skal utvikle et repertoar av strategier for å løse matematiske problemer, og at de skal oppleve at matematikk er mer enn å bruke faste innlærte metoder til å løse bestemte typer oppgaver. Det gjelder ikke bare å huske regler og prosedyrer, men å være kreativ og våge å prøve seg fram og gjøre sine egne erfaringer.



Et slikt arbeid er også en utfordring for læreren. Her kan problemstillingene ta mange ulike retninger, og det finnes ingen fasit. Vi oppmuntrer også læreren til å våge å la elevene ta styring over utforskningsarbeidet.



I dette opplegget vil ulike elever utfordres på ulike nivåer. For noen elever vil det være et mål å kunne se og beskrive mønsteret i 2 x 2-kvadrater og kanskje utvide det til større kvadrater. Det kan være en hjelp å få tips om at resultatene kan fylles inn i en tabell.

For andre elever vil det være en passende utfordring å finne et system i alle rektangler og kvadrater. når de kjenner systemet, kan de da si hvilke rektangler som gir et bestemt svar på regnestykket?



Elevene utfordres også til å bevise de ulike systemene ved å bruke algebra for å generalisere. noen elever vil kanskje utvikle mønster i andre figurer enn kvadrater og rektangler. De vil støte på nye, men tilsvarende problemer.



Læreplanen sier at "problemløysing høyrer med til den matematiske kompetansen. Det er å analysere og omforme eit problem til matematisk form, løyse det og vurdere kor gyldig

det er. Dette har òg språklege aspekt, som det å resonnere og kommunisere idear". Dette

er ferdigheter som må øves gjennom matematikkundervisningen på alle trinn. i dette

opplegget refererer vi til kompetansemål i r2, men det er viktig at elevene tidlig får erfaring

med problemløsning. opplegget med hundrekartet gir problemstillinger som kan passe for

ulike nivåer og klassetrinn.



På de neste sidene er gangen i arbeidet med en slik undersøkelsesoppgave skissert. Det er

ikke laget elevark med oppgaver til dette emnet. Her skal elevene få arbeide mest mulig fritt.

Pass på at det settes av tid i slutten av økta til oppsummering.

Gangen i arbeidet



Del først ut hundreark og brikker til elevene: (Kopieringsorginal)

1) Be elevene om å legge brikkene slik at de danner et 2 x 2-kvadrat, hvor som helst på hundrekartet. Nedenfor finner du to eksempler på plassering av brikkene.

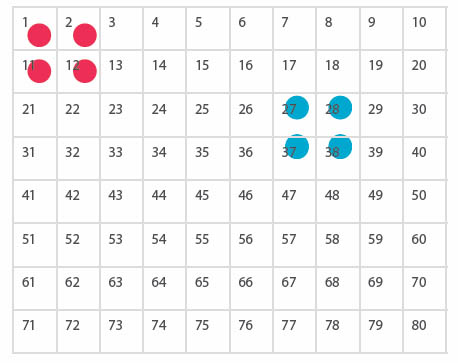
Gi elevene instruksjonene nedenfor. Be dem om å skrive hvilke tall de velger, og utregningene de gjør.



Elevene skal bruke de fire tallene i rutene til et regnestykke etter et bestemt mønster:

Tallene som danner en diagonal fra øvre høyre til nedre venstre hjørne multipliseres med hverandre. Trekk så ifra produktet av tallene i den andre diagonalen.



Be elevene om å finne svaret på regnestykket i eksempelet ovenfor: 2 • 11 – 1 • 12 =



Sammenlikn svarene elevene har fått. Be elevene undersøke hva som skjer når de legger stadig større kvadrater på hundrekartet. Mange kan trenge hjelp til å velge strategier som kan være nyttige for å se systemer. Én slik strategi er å sette resultatene opp i en tabell:

2) Etter at elevene har arbeidet en stund med dette, kan det passe å ta en plenumssamtale.

Hva har de oppdaget? ser det ut til å være noe system her?

NB! Vent med å forklare eller vise systemet generelt for alle. Det er viktig å forsikre seg om at alle har forstått hva de skal gjøre.

3) Be elevene fortsette undersøkelsen av liknende tilfeller. Det betyr at elevene selv må bestemme seg for hva slags lignende tilfeller de vil fortsette å undersøke. noen vil komme til å legge stadig større kvadrater, andre vil legge rektangler. Det er også mulig å legge fire brikker i andre mønster.

Utfordring til elevene

Formuler skriftlig hva du vil fortsette å undersøke.



Formuler også dine egne gjetninger:

Tror du resultatene vil følge et bestemt mønster?

i tilfelle: Hvilket mønster? sjekk om det stemmer.

Skriv ned det du erfarer og finner ut.

4) Prøv å hjelpe elevene til å finne ut mest mulig selv. Mange kan trenge hjelp til

å velge strategier som kan være nyttige for å se systemer.

5) Når elevene har funnet en del systemer, er det tid for å generalisere og vise hvorfor alle kvadratene med samme størrelse gir samme svar.

Anbefal dem å begynne med det enkleste - kvadratet fra pkt. 1.

Hvordan vil de bygge opp et slikt bevis?

a)      Det må først presiseres hva man vil bevise. Be elevene skrive det som en påstand som skal bevises.

b)      Et bevis skal gjelde generelt, så de må generalisere. gi elevene et hint: Kall tallet i en av rutene for a.

         Kan tallene i de andre rutene uttrykkes ved hjelp av a?

c)      Regn ut det generelle tilfellet etter de samme reglene som før. Blir systemet bekreftet?

d)     Skriv til slutt en konklusjon, den skal relateres til påstanden.

Tilsvarende metode kan brukes til å bevise systemene som skapes dersom brikkene legges ut i andre mønster.

Forberedelse til oppsummering og oppsummering



• Har elevene sett ulike systemer? Hvilke?

• Hvilke strategier har de brukt?

• Hva må til for å sette opp et bevis?



Finn i løpet av økta noen elever som kan presentere arbeidet sitt i oppsummeringen. Slik kan man få belyst flere måter å løse problemene på, elevene får øving i å vise og begrunne strategiene sine og eksemplene som trekkes fram kan brukes til en konklusjon.



Forslag til løsninger

Forklaring ved hjelp av algebra:

Hvis vi velger et kvadrat av fire ruter hvor som helst i hundrekartet, og kaller tallet i øverste venstre rute for a, hvordan kan vi da skrive tallene i de tre andre rutene ved hjelp av a?

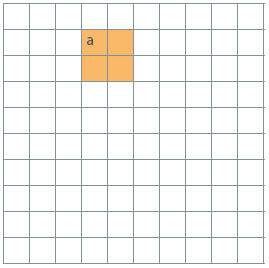
Lag nå et regnestykke etter samme regler som i forrige oppgave, men bare ved hjelp av de fire talluttrykkene som inneholder a. Hva blir svaret i dette regnestykket? Stemmer det med det du fant ut i forrige oppgave?

Tallene i de fire rutene kan skrives slik:

Og regnestykket blir:

(a + 1) · (a + 10) – a · (a + 11) =

a² + a + 10a + 10 – a² – 11a = 10

Dette vil alltid gjelde i 2 x 2–kvadrater i hundrekartet. Vi har vist det for et generelt tilfelle.

Oppgave

Elevene kan for eksempel utvide denne oppgaven ved å lage stadig større kvadrater:

Legg brikkene i hjørnene av et 3 x 3-kvadrat:

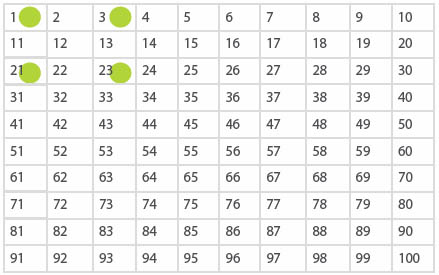
• Vi lager regnestykke etter samme mønster:
  
  Multipliser tallet i øvre høyre hjørne med tallet i nedre venstre hjørne og trekk fra produktet av tallene i øvre venstre hjørne og nedre høyre hjørne.
  
  I eksempelet over blir regnestykket 3 • 21 – 1 • 23 =
  
  Hva blir svaret?
• Legg brikkene ut i samme mønster på andre steder på hundrekartet, lag regnestykker
  
  og regn ut. Hva ser du?
• Prøv å forklare hvorfor det blir slik du ser. Du kan forklare med ord eller på algebraspråket (dvs. med bokstaver).
• Hva skjer hvis vi i stedet for kvadrater legger brikkene ut i rektangelform?
• Hva blir svaret på regnestykket om vi lager et 2 x 3–rektangel?
• Både de turkise og de oransje brikkene nedenfor ligger i 2 x 3-mønster, men ikke på samme måte. Vi kan godt kalle formene 2 x 3 og 3 x 2. Blir det forskjell på svarene i
  
  regnestykkene i de to tilfellene? 

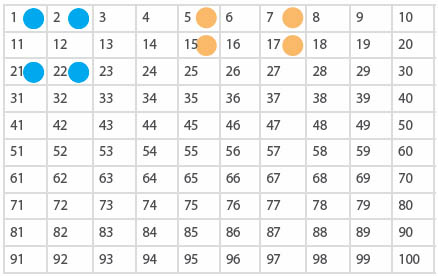
Oppgave

• Kan du legge brikkene i rektangler slik at svaret på regnestykket blir 30? Hvordan må de eventuelt legges da?
• Kan du legge brikkene slik at svaret blir 50? enn 60? 70? 80? 90? Forklar hva du gjør!
• Er det noen av disse oppgavene som kan løses på flere måter, dvs. ved å legge ulike rektangler?

Generalisering

Vi tenker oss igjen at vi starter i et tilfeldig valgt tall a. så tenker vi oss at vi legger brikkene i et tilfeldig valgt rektangel med bredde b og høyde h. Det betyr at tallet i øvre høyre rute blir a + (b – 1) og i nedre venstre hjørne a + 10 (h – 1). Hvorfor blir det slik?

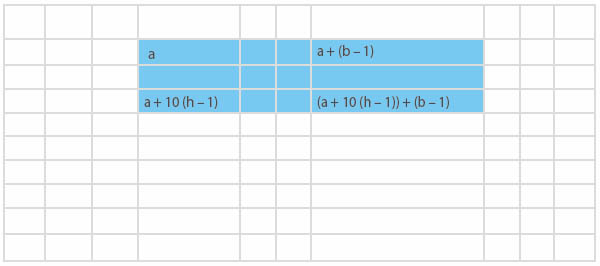
• Finn svaret på regnestykket i hundrekartet på forrige side.
• Forklar hvorfor løsningen ikke er avhengig av tallet a som vi tok utgangspunkt i.
• Sammenlikn løsningen du har fått her med det du har regnet ut tidligere. Stemmer den generelle løsningen med utregningene du har gjort i eksemplene ovenfor?
• Den generelle løsningen kan skrives som 10(b – 1) (h – 1).
• Forsøk å arbeide med svaret du fikk til du får det på denne formen.
• Forklar hvorfor denne løsningen sier oss at vi får samme svar om et rektangel ”ligger”
  
  eller ”står på høykant”, bare det er like stort.

Andre muligheter for å utvide oppgaven

- I stedet for et 10 x 10–ark, kan vi bruke 7 x 7, 8 x 8 eller 9 x 9 osv.

- Vi kunne også ha forsket på hva som skjer om vi legger andre former enn rektangler.