Kvikkbilde - tallfølger
Emne
Tallfølger
Hensikt
Elevene skal systematisere og overføre et visuelt mønster, via tallmønster, til en rekursiv og en eksplisitt formel for leddene i en tallfølge.
Valg av tidspunkt
Du trenger
En PC og prosjektor til å vise et kvikkbilde.
Aktiviteten
Arbeidsform:
Individuelt arbeid først. Deretter deler elevene sine løsninger med sidemannen.
Undervisningsopplegget:
Forklar elevene at de skal se nøye på et bilde som de får se i tre sekunder. Si at de skal legge merke til hvordan figurene er bygd opp, og hvordan de «vokser». Gi elevene god tid til å tenke og notere. Deretter viser du bildet på nytt i tre sekunder. Elevene får mulighet til å revidere det de har tenkt og skrevet. De to første spørsmålene under «oppgave» kan stå på tavla hele tiden. Under oppsummeringen står alle spørsmålene på tavla.
Når elevene har tenkt ferdig, lar du bildet bli stående mens elevene får forklare sine løsninger.
Her er bildet:
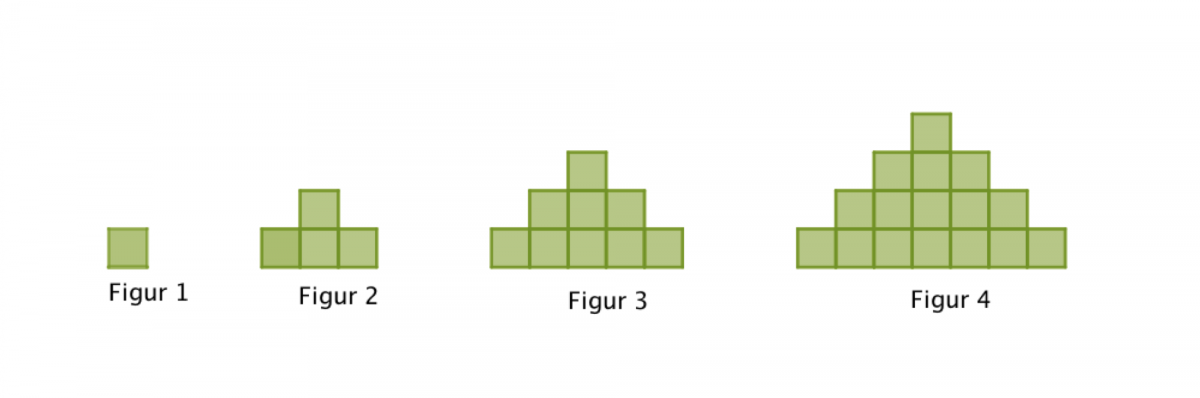
Oppgave:
Mens elevene ser kvikkbildene skal de bare prøve å finne svar på følgende spørsmål:
- Hvordan er mønsteret du får se bygd opp?
Når bildet blir stående, og dere skal ha oppsummering, får elevene disse spørsmålene i tillegg.
- Hvordan kan du tegne neste figur hvis du har den forrige?
- Hvis antall kvadrater i hver figur skrives som et tall, hvordan kan du beregne det neste tallet ut fra det foregående? Skriv tallet til figur n rekursivt med ord og symboler/formel.
- Hvordan kan du beregne tallet som figur nummer n representerer direkte (eksplisitt)? Finn en formel.
Kommentarer til læreren:
Elevene må få god tid til å tenke og skrive. Når det har gått en stund etter at bildet ble vist for annen gang, lar du elevene snakke sammen to og to.
Eksempler på elevsvar
Eksempel 1
Eleven sier at nye kvadrater blir bygd rundt de som er der fra før. Du starter med 1 og legger på 3, deretter 5 og 7 og så videre. Eleven viser med farger, omtrent slik:

For hver nye figur, blir det lagt til et oddetall.
Eleven kommer fram til den rekursive formelen: an = an-1 + (2n - 1).
Kommentar: Kanskje elevene vil ha problemer med å nummerere riktig. Det kan dere snakke om i oppsummeringen.
Eksempel 2
Eleven sier at figurene kan «klippes og limes» til kvadrater. I figur 2 klippes og flyttes det lille kvadratet på høyre side og limes i øverste venstre hjørne. Da blir det et 2·2 kvadrat. I figur 3, klippes de tre kvadratene på høyre side, snues og limes øverst til venstre. Da blir det et 3·3 kvadrat. På samme måte klippes, snues og limes de fem kvadratene til høyre i figur fire, så det blir et 4·4 kvadrat. Eleven tegner omtrent slik:
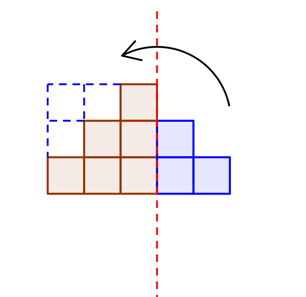
Eleven kommer fram til den eksplisitte formelen: an= n ∙ n = n2
Kommentar: Denne eleven ser hvordan hver enkelt figur er bygd opp, og kommer fram til en eksplisitt formel.
Eksempel 3
Eleven sier: De blir først 1, så 1 + 2 + 1, så 1 + 2 + 3 + 2 + 1, så 1 + 2 + 3 + 4 + 3 + 2 + 1 og så videre.
Kommentar: Utfordre eleven og de andre i klassen til å skrive summen som viser figurtall nummer n med symboler når dere tar oppsummering.
Eksempel 4
Eleven sier: Jeg ser at hver figur er summen av oddetall. Figur nummer n er 1 + 3 + 5 + 7 +…+ (2n - 1)
Kommentar: Dette eksempelet sammen med eksempel 2, gir dere en fin mulighet til å se at summen av oddetallene er et kvadrattall, og derfra mer generelt, komme fram til formelen for summen av de n første leddene i en aritmetisk rekke.
Oppsummering:
Pass på at alle de ulike forslagene kommer fram, og skriv dem på tavla slik elevene forklarer dem. La eventuelt elevene komme fra og skrive på tavla selv. Det bør bli plass til at alle eksemplene kan stå på tavla samtidig.
Utfordre klassen til å sammenlikne alle forslagene. Er de like? Er de forskjellige? Kan alle skrives med rekursive og eksplisitte formler?
Hvis både eksempel 2 og eksempel 4 kommer fram, kan du utfordre elevene til å bevise at
1 + 3 + 5 + 6 +…+ (2n - 1) = n2
Senere kan dere sammen vise at den ideen som brukes til å bevise dette, er den samme ideen som kan brukes til å bevise formelen for summen av de n første leddene i en aritmetisk rekke.
Eksempel 3 er også morsomt å se nærmere på.
Figur nummer n kan skrives: 1 + 2 + 3 +…+ (n - 1) + n + (n - 1) +…3 + 2 + 1
Du kan introdusere summetegnet for elevene, og vise at eksempel 4 kan skrives slik:
`a_(n)=sum_(i=1)^n(2i-1)`
og eksempel 3 slik:
an = n + 2 ∙ `sum_(i=1)^(n-1) (i)`
når n≥2
Vurdering:
La elevene skrive eksempel på en tallfølge, med eksplisitt og rekursiv formel. Samle inn eksemplene og se om alle har forstått begrepene.
Forslag til videre arbeid:
Arbeid videre med figurtall. Elevene kan lage sine egne figurer med brikker. Utfordre dem til å sette opp rekursiv og eksplisitt formel for figurtallene.
Rammeplanmål/Kompetansemål
- Videregående
- R2
- gi eksempler på ulike situasjoner som kan modelleres ved å bruke ulike matematiske funksjoner, og modellere og analysere slike situasjoner ved å bruke reelle datasett
- utforske egenskaper ved ulike rekker og gjøre rede for praktiske anvendelser av egenskaper ved rekker
- S1
- uttrykke egne resonnementer ved hjelp av matematiske begreper og symbolspråk
- S2
- utforske egenskaper ved ulike rekker og gjøre rede for praktiske anvendelser av egenskaper ved rekker
