Prisme i 3D
Emne
To- og tredimensjonale figurer, volum, overflate, GeoGebra, prisme, 3D-briller.
Hensikt
Elevene skal få varierte erfaringer med tredimensjonale figurer ved å studere sammenhengen mellom todimensjonale tegninger og tredimensjonale figurer. De skal også øve på å tolke en bruksanvisning, samt beskrive og forklare hva de ser for medelever.
Valg av tidspunkt
Du trenger
Aktiviteten
Introduksjon
Start timen med en samtale om prismer. For eksempel: Hvordan ser et prisme ut, grunnflate, toppflate, volum, overflate og eventuelt noen formler. Det kan også være hensiktsmessig å se på sammenhengen mellom prisme og kube siden det ikke er selvsagt for alle elever at en kube er et spesialtilfelle av et prisme.
Opplegget er laget slik at elevene, etter en kort innføring, jobber seg parvis gjennom et elevark . Det er en fordel at elevene gjør GeoGebra brukervennlig ved at de velger at GeoGebra skal vise hjelpelinje og ikke sette navn på nye objekt (se GeoGebrahjelp nederst på siden).
Elevene jobber selvstendig med elevarket som inneholder en oppskrift. Elevene må lese en matematisk tekst og tolke det som står der, samtidig som de utfører oppgaven i GeoGebra. Selv om elevene jobber med hver sin PC, skal de jobbe sammen parvis eller i smågrupper. Det er viktig at de diskuterer med hverandre hvordan de skal tolke instruksjonen. Først når de har diskutert og prøvd, kan de spørre læreren. Før læreren svarer, er det viktig at hun sjekker om alle elevene i gruppen har det samme problemet. På den måten kan hun være mer sikker på at elevene jobber sammen og trener på å forklare for hverandre.
Elevarket inneholder de samme tegningene som denne beskrivelsen av opplegget, men her står det i tillegg noen tips og henvisninger til vanlige feil og misforståelser.
Utforsking og kommentarer til læreren
Elevene åpner en ny fil i GeoGebra og velger å vise både rutenett og koordinatsystem.
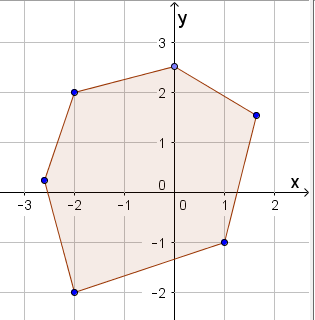
Så tegner de en Mangekant rundt origo. Antall hjørner spiller ingen rolle, men pass på at mangekanten ikke er for stor. Årsaken er at vi ønsker at elevene skal se hele figuren når de åpner Grafikkfelt 3D.
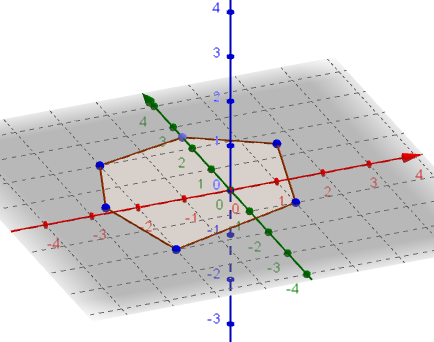
Elevene åpner så Grafikkfelt 3D. Da får de se figuren som de har tegnet. Den ligger «på gulvet», altså i xy-planet. Elevene skal nå flytte på hjørnene til figuren både i Grafikkfelt og i Grafikkfelt 3D for å se om de ser sammenhengen mellom vinduene?
For elevene er begrepet "xy-plan" ukjent, men de har tegnet mange grafer med x- og y-akse. Derfor kan det være fint for elevene å se at det de har jobbet med i 2D, finner de igjen i 3D. Ordet "gulvet" gir mening. Hvis elevene ikke finner figuren i Grafikkfelt 3D, må de høyreklikke i vinduet for å kontrollere om GeoGebra viser vinduet i Standard visning.
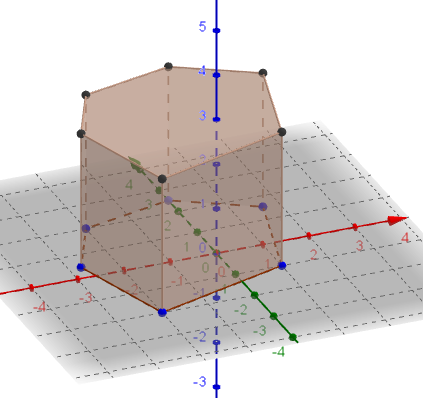
Grafikkfelt 3D har verktøyknapper som er forskjellig fra verktøyknappene i Grafikkfelt. Elevene åpner undermenyene i knappen med pyramiden og velg Ekstruder til prisme eller sylinder.
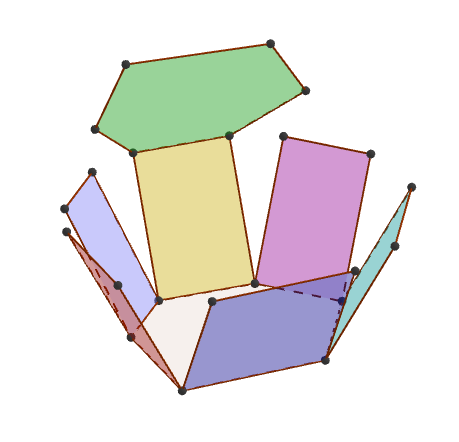
Så klikker de på mangekanten og skriver inn et lite tall (3, 4 eller 5) som høyde i tekstboksen. Da får de en figur som ligner figuren på bildet. Ved å velge et lite tall for høyden, slipper elevene å endre størrelsen til Grafikkfelt 3D. Det er imidlertid mulig å endre størrelsen i Grafikkfelt 3D ved å høyreklikke i feltet og velge Forstørr eller forminsk.
Elevene skal nå passe på at Flytt er aktivert, og deretter klikke på den lille trekanten foran Grafikkfelt 3D. Da ser de en ny verktøylinje. Ved å klikke på de tre knappene til venstre, forsvinner koordinataksene, rutenettet og «gulvet».
Disse endringene gjør at figuren ligner mest mulig på figurene i lærebøkene. Hvis figuren er i en boks, kan de fjerne boksen med andre knapp fra høyre. Elever som ikke finner verktøylinjen har enten glemt å aktivere Flytt eller glemt å klikke på trekanten foran Grafikkfelt 3D.
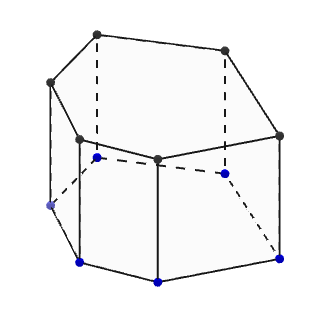
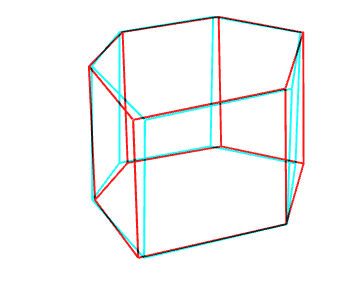
Elevene må igjen kontrollere at Flytt er aktivert. Så finner de ordet Prisme i Algebrafelt og klikker på det. Hele figuren blir da markert. Elevene skal så gi figuren svarte kanter med så lite fyll som mulig. Det er viktig at de ikke tar bort all farge for da vil det ikke være mulig å se forskjell på synlige (heltrukkede) og usynlige (stiplede) linjer.
Ved å venstreklikke og bevege musa i Grafikkfelt 3D kan elevene bevege prismet, og elevene skal undersøke hva som skjer med de synlige og usynlige kantene. Figuren ligner nå på figurene elevene kjenner fra læreboka, og når elevene snur på figuren vil de synlige og usynlige kantene hele tiden tilpasse seg automatisk. Elever som trenger ekstra utfordring kan jobbe med hele linjer (fjerne all farge slik at både synlige og usynlige linjer blir heltrukkede).
Etter at elevene har studert prismet i ulike posisjoner, skal de snurre figuren tilbake til utgangspunktet.
Elevene klikker på trekanten ved knappen lengst til høyre i verktøylinjen under Grafikkfelt 3D og finner fram til knappen med brillene.
Figuren blir da utydelig, og de må se på figuren med 3D-briller.
Elevene vil se at figuren "kommer ut fra" PCen, og det blir lettere å se sammenhengen mellom en tredimensjonal figur og figuren i læreboka. 3D-brillene gjør at alle figurer vil se grå ut.
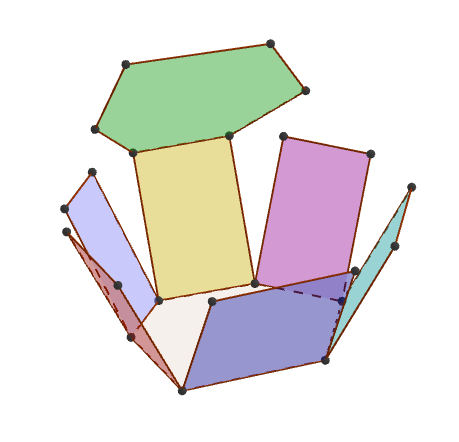
Deretter skal elevene finne verktøyknappen BrettUt (på samme undermeny som Ekstruder til prisme eller sylinder) og klikke på figuren. Prismet vil da bli brettet ut slik at elevene kan studere overflaten. Det blir samtidig laget en glider i Grafikkfelt, og ved å eksperimentere med glideren kan elevene undersøke overflaten ytterligere. Ved å høyreklikke på glideren og sette Animasjon på skjer utbrettingen automatisk i lavt tempo.
Elevene kan ta av 3D-brillene og vise den vanlige figuren. Da kan det være fint å fargelegge de forskjellige sidene.
Funksjonen BrettUt fungerer bare på figurer basert på mangekanter. Den lager et nytt lag utenpå prismet, og det kan forvirre noen elever. Da er det best å gjøre prismet usynlig ved å høyreklikke på prismets navn i algebrafeltet og trykke på Vis objekt slik at GeoGebra bare viser overflaten. På den måten samsvarer figuren bedre med elevenes forestilling.
Hvis elevene har tegnet en mangekant med konkave hjørner, fungerer ikke verktøyet BrettUt. Eleven må da flytte på hjørnene i mangekanten slik at alle hjørner blir konvekse.
Utforske videre
Når elvene har laget og undersøkt prisme i 3D, kan de utforske andre figurer. Det finnes verktøyknapper for blant annet kule, terning og tetraeder i Grafikkfelt 3D, og elevene trenger ikke å gå veien om Grafikkfelt når de bruker disse. La elevene prøve seg fram.
På elevarket foreslår vi en oppgave som går ut på å tegne en terning med en kule inni. Figuren er lettest å tegne ved at elevene legger kvadratet som utgjør grunnarealet til terningen rundt origo. Utfordringen blir å finne sentrum og radius til kula.
Vær oppmerksom på at GeoGebra ikke oppfatter en sirkel i Grafikkfelt som en sirkelflate, men bare som en kurve. Elevene kan derfor ikke klikke på arealet til sirkelen. Hvis de derimot aktiverer Ekstruder til prisme eller sylinder og så klikker på sirkellinja i Grafikkfelt 3D blir sirkelen endret til en sirkelflate og tekstboksen for å skrive inn høyden vises.
Til utforskning er det viktig at GeoGebra viser hjelp for verktøylinjen. Da kommer det opp en tekst ved siden av verktøylinjen som forteller hva knappene er til, og det gjør det lettere for elevene å vite hvilke knapper de skal bruke og hvordan.
Oppsummering
Læreren avslutter aktiviteten med en felles oppsummering. Aktuelle spørsmål til elevene kan være: Hva lærte dere i denne aktiviteten? Hvordan kan dere bruke disse erfaringene når dere arbeider med todimensjonale tegninger av tredimensjonale figurer? Hva var vanskelig? Hva var lett? Hva diskuterte dere i gruppene? Det kan også være aktuelt å velge ut noen grupper som viser fram sin figur og forklarer prosessen, utfordringene og diskusjonene de har hatt underveis.
GeoGebrahjelp
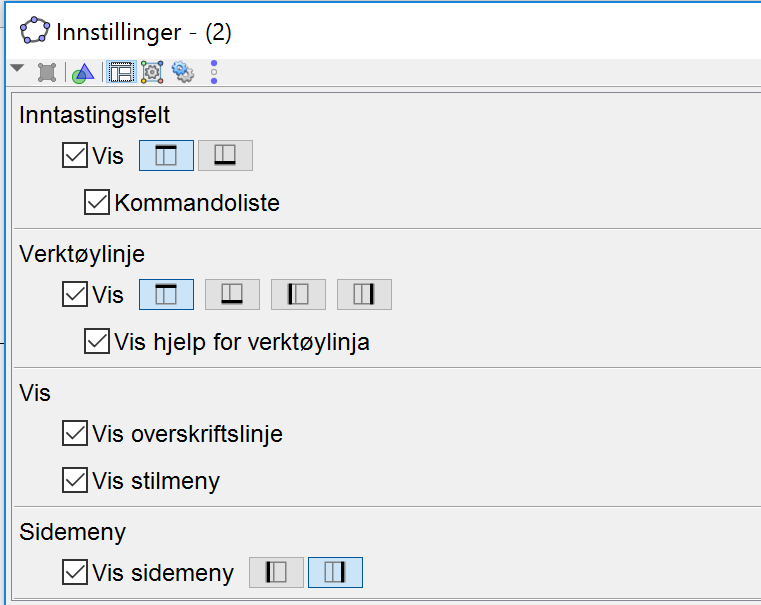
For å endre innstillinger, klikker elevene på tannhjulet i øvre, høyre hjørne eller høyreklikker i Grafikkfelt eller Grafikkfelt 3D og velger Grafikkfelt. Deretter velger de Utforming, og krysser av for Vis hjelp for verktøylinja.
For læreren er det viktig at Inntastingsfelt står øverst, og det kan hun velge i øverste felt.
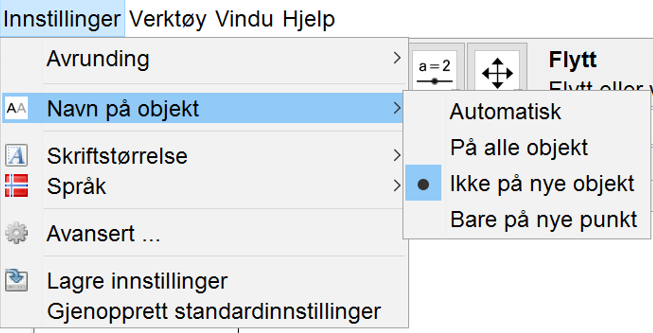
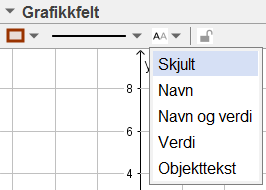
GeoGebra gir automatisk alle nye objekt en etikett med navn i Grafikkfelt og Grafikkfelt 3D. Det blir fort uoversiktlig, og derfor er det lurt å krysse av for Ikke på nye objekt under Innstillinger. Elevene kan hente navn og verdi etter behov. I Grafikkfelt 3D kan det hende at GeoGebra setter navn på nye objekt likevel, men elevene kan ta bort disse.
Ved å klikke på Lagre innstillinger, slipper elevene å gjøre denne prosedyren hver gang.
I GeoGebra er det mulig å endre endre farge, linjestil og benevning på objekt. Først markerer elevene objektet de vil endre, og deretter velger de hva de vil endre. Hvis verktøylinjen ikke er synlig, må elevene klikke på den grå trekanten til venstre for ordet "Grafikkfelt".
Rammeplanmål/Kompetansemål
- Grunnskole
- Kompetansemål etter 6. trinn
- beskrive eigenskapar ved og minimumsdefinisjonar av to- og tredimensjonale figurar og forklare kva for eigenskapar figurane har felles, og kva for eigenskapar som skil dei frå kvarandre
- Kompetansemål etter 9.trinn
- utforske eigenskapane ved ulike polygonar og forklare omgrepa formlikskap og kongruens
- Videregående
- Vg1P
- bruke digitale verktøy i utforsking og problemløysing knytt til eigenskapar ved funksjonar, og diskutere løysingane
- modellere situasjonar knytte til tema frå samfunnsliv og arbeidsliv, presentere og argumentere for resultata og for når modellane er gyldige
- utforske, beskrive og bruke omgrepa proporsjonalitet og omvend proporsjonalitet
- Vg1T
- formulere og løyse problem ved hjelp av algoritmisk tenking, ulike problemløysingsstrategiar, digitale verktøy og programmering