Pytagoras sin vimpelrekke

Dynamisk geometri, rettvinklet trekant, Pytagoras’ setning, areal

PC med GeoGebra

Oppgave til elevene

• Tegn et kvadrat. Vis arealet og beveg slik at arealet blir 1.
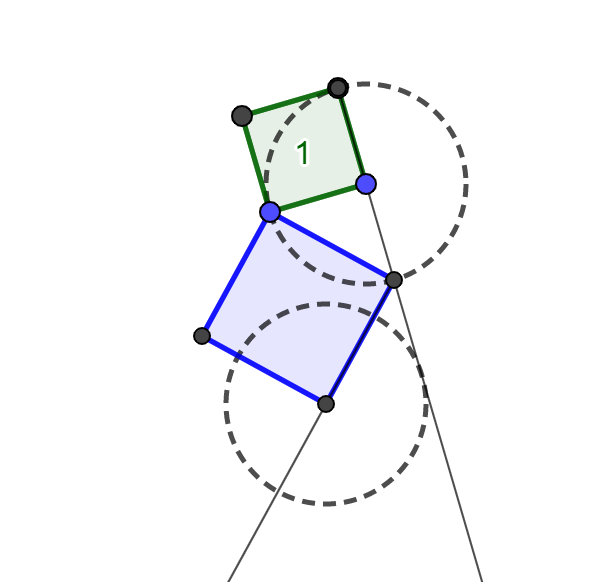
• Lag konstruksjonen slik som på bildet:

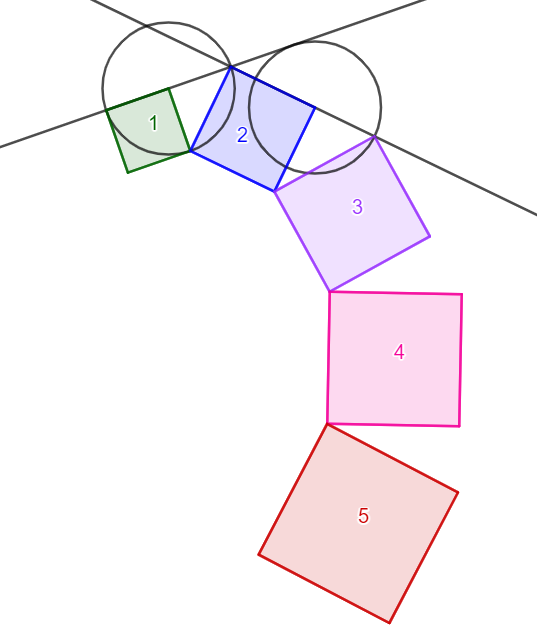
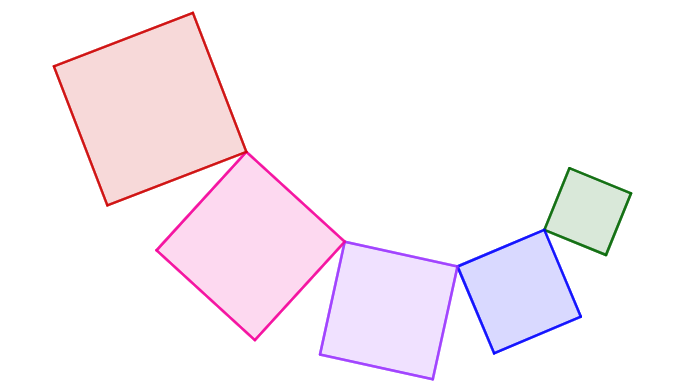
• Fortsett på samme måte til du har minst fem kvadrater.
• Vis arealet til kvadratene.
• Dra i start-kvadratet. Hva skjer?

Kommentar til læreren

Start med en klassesamtale om summen av kvadrater. Bruk erfaringene fra Kvadrat + kvadrat = kvadrat dersom elevene har gjort den aktiviteten. Hvilket areal har et kvadrat hvis det er summen av to kvadrater med areal 1? Hvordan vil dere tegne et slikt kvadrat? Hva med et kvadrat med areal 3, areal 4, areal 5 og så videre? Elevene skal komme fram til at de kan bruke Pytagoras’ setning og et kvadrat med areal 1 (sidelengde 1). Kvadratene er arbeidskrevende å tegne på papir, men i GeoGebra går det ganske raskt.

For å få en dynamisk figur som er lett å utforske, lager elevene et vilkårlig kvadrat, for eksempel med Regulær mangekant. Hvis de starter med et kvadrat med side og areal 1 blir figuren statisk. Elevene kan se starten på konstruksjonen på bildet. På bildet er Stråle gjennom to punkt brukt for å forlenge sidene til kvadratene, men elevene kan også bruke Linje. Underveis i arbeidet kan det være lurt å gjøre hjelpelinjene usynlige. Da er det enklere å beholde oversikten. Tips elevene om verktøyet Passer som gjør det lett å sette av lengder.

Forslag til konstruksjon:

Oppsummering

Når elevene har laget og utforsket figuren sin, forsetter økten i hel klasse. Studer og diskuter oppdagelser elevene har gjort. For eksempel hvordan arealet endrer seg hvis start-kvadratet har areal 4, hvor store arealene er hvis start-kvadratet er 1,5 eller hvordan sidelengden øker når start-kvadratet har sidelengde 1. Støtt elevene i å finne forklaringer på hvorfor det er slik. Kanskje noen elevpar har laget figurer som oppfører seg annerledes. Hva er grunnen til det? Elevene kan også lage formler som for eksempel beskriver hvordan arealet øker.