Regresjon med GeoGebra

GeoGebra, funksjon, regneark, grafisk framstilling, stolpediagram, søylediagram, regresjon

PC med GeoGebra installert, elevark GeoGebra 5 eller elevark GeoGebra 6,  og PowerPoint-presentasjon.

Aktivitet 1

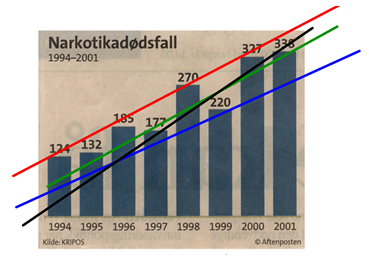
Figur 1: Stolpediagram som viser narkotikadødsfall i perioden 1994-2001

Opplegget starter i hel klasse. Læreren viser fram figur 1 (se PowerPoint-presentasjon) på en Whiteboard slik at det er mulig å tegne på figuren. I en klassesamtale skal elevene beskrive hva de ser og hva de tror kommer til å skje. Mange elever vil tro at antallet narkotikadødsfall øker også i fremtiden.

Kommentarer til læreren

Elevene kan tegne inn linjer som viser hvordan de tror utviklingen blir. Læreren bør oppfordre elevene til å være konkrete når de forklarer hvordan de tror linjene skal se ut. For eksempel at linja skal ligge over hver søyle, at den skal ligge midt i mellom alle verdiene eller at den skal gå fra laveste til høyeste verdi. Be gjerne elevene om å anslå et antall for 2012 (eller et annet år som har vært, slik at det er mulig å sjekke det faktiske antallet).

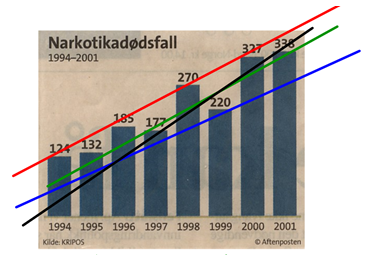
Etter klassesamtalen, kan et tavlebilde se ut som figur 2. Erfaring viser at mange elever tenker slik som det grønne eksempelet, nemlig å lage en slags gjennomsnittslinje.

Mulige elevkommentarer til de forskjellige linjene kan være:

• Denne linja ligger for høyt. (rød linje)
• I 1994 er det over 120 dødsfall. Denne linja starter for lavt. (svart linje)
• Denne linja kan være ganske riktig. Det har noen verdier over og noen under. (grønn linje)
• Det må bli flere enn dette. Linja ligger under hele veien. (blå linje)

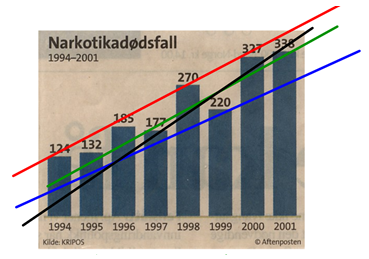
Figur 2: Forslag til regresjonslinjer

Aktivitet 2

Elevene kan bruke GeoGebra til å finne linja som passer best til verdiene. Læreren må tilpasse veiledningen til hvor mye elevene kan fra før. Vi anbefaler at elevene arbeider i smågrupper slik at de kan diskutere og hjelpe hverandre.

Elevene skal først tegne et stolpediagram, og deretter finne linja som passer best til verdiene. Vi har valgt å lage to utgaver av elevarket, ett for GeoGebra 5 og ett for GeoGebra 6, siden fremgangsmåten for å tegne stolpediagram er forskjellig.

Kommentarer til læreren

Mange elever vil skrive inn årstallene i regnearket. Når de så overfører stolpediagrammet til Grafikkfeltet, kommer stolpediagrammet langt unna origo. For å få stolpediagrammet nærmere origo, kan de velge år 1994 som år 4, 1995 som år 5 og så videre. De kan også velge 1994 som år 0, men da blir det litt vanskeligere å bruke regning for å finne rett årstall.

Aktivitet 3

Etter at elevene har funnet ei linje som passer til verdiene, fortsetter opplegget i hel klasse. Målet er å sammenligne linja som GeoGebra har tegnet med forslagene som klassen kom fram til, samt å drøfte hva linja forteller oss om antall narkotikadødsfall før og etter de oppgitte årstallene.

Hvordan stemmer resultatet fra beregningene i året 2010 og 2016? Læreren viser elevene nyere statistikk over antall narkotikadødsfall fra SSB (se figur 3). Målet er å diskutere forskjellen mellom det teoretiske svaret og virkeligheten. Elevene har fått et riktig matematisk svar, men svaret stemmer ikke overens med virkeligheten.

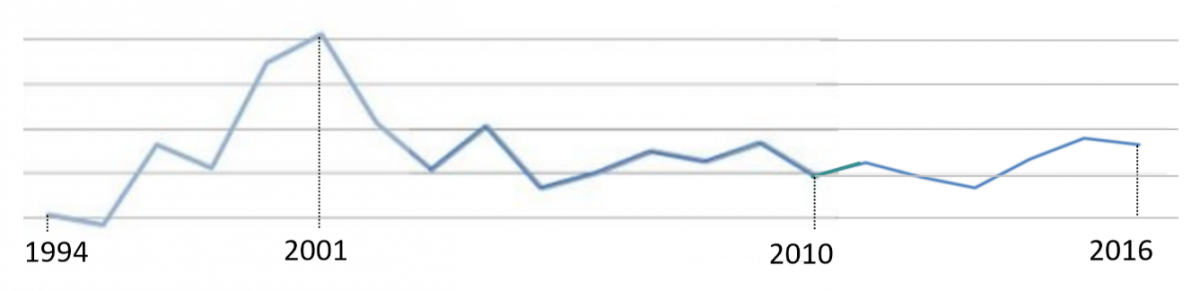
Figur 3: Narkotikadødsfall i perioden 1994-2016

Kommentarer til læreren

Relevante spørsmål i diskusjonen kan være:

• Hva betyr stigningstallet til funksjonen?
• Hvor mange narkotikadødsfall vil det bli i 2010 eller i 2016?
• Hvor mange dødsfall var det i 1980 etter denne modellen?
• Hva skjer hvis elevene utelater verdien for 1994 og 1995? Blir svaret det samme?

Elevene kan finne ut hvor mange dødsfall det blir i 2010 ved å skrive x = 20 (hvis 1990 er år 0) og finne skjæringspunktet med grafen. Det klarer de fleste elevene. Men svaret stemmer bare hvis utviklingen fortsetter på samme måte, og det gjør den ikke i dette tilfellet.

1980 gir et negativt svar. Hva betyr det? Resultatet viser at elevene må se på gyldighetsområdet til modellen. Vi kan ikke si noe om antallet før den første målingen.

Elevene kan også diskutere årsaker til nedgangen og deretter relativt stabilt antall narkotikadødsfall. Kan det være innsats mot narkotika på skoler, flere politifolk ute på patrulje, sykepleiere ute i byen, nye sprøyterom eller strengere straff ved salg?

Veien videre

Elevene kan utforske statistikk fra mange forskjellige fagfelt på denne måten. Eksempler er forbruk pr husholdning, folkeutvikling i kommunen de bor i eller Norges utslipp av klimagasser. Elevene kan finne relevant data på nettsidene til Statistisk sentralbyrå (www.ssb.no).