Sammenhengen mellom arealet og omkretsen til et rektangel
Emne
GeoGebra, geometri, rektangel, areal, omkrets, algebra, funksjoner
Hensikt
Opplegget skal gi elevene en bedre forståelse av egenskapene til rektangler gjennom å utforske sammenhengen mellom areal og omkrets.
Valg av tidspunkt
Du trenger
Hver elev trenger en PC med GeoGebra.
Aktiviteten
Opplegget består av tre aktiviteter elevene skal gjøre i GeoGebra. Aktivitetene forutsetter at elevene kan tegne i GeoGebra. Elevene skal først tegne en figur som er et rektangel uansett hvordan de snur og vender på den. Deretter skal de tegne et rektangel med fast omkrets, og til slutt skal de finne det største arealet som et rektangel med en gitt omkrets kan ha.
Elevene jobber med hver sin PC, men de kan gjerne sitte i små grupper slik at de kan diskutere underveis.
Aktivitet 1: Tegn et rektangel
Oppgave 1 til elevene
- Åpne GeoGebra og tegn et rektangel.
- Dra i hjørnene til rektangelet. Hva skjer?
Kommentarer til læreren
Mange elever bruker verktøyet Mangekant og tegner et rektangel på rutearket i GeoGebra, mens noen bruker Linjestykke mellom to punkt. Figurene de da får er ikke rektangler, men mangekanter som tilfeldigvis har form som rektangler. Når elevene tester figurene ved å dra i hjørnene, blir figurene til uregelmessig firkanter.
Klassesamtale
Aktiviteten fortsetter med en klassesamtale om egenskapene til et rektangel. Resultatet kan se omtrent slik ut:
Et rektangel er en firkant der
- To og to sider er like lange
- To og to sider er parallelle
- Alle vinkler er 90°
- Diagonalene er like lange
- Diagonalene halverer hverandre
Rektangler har alle disse egenskapene, men må elevene bruke alle egenskapene for å tegne et rektangel, eller er det nok med en eller to? Elevene skal diskutere i smågrupper for å finne ut hvor mange egenskaper de trenger for å tegne et rektangel. For eksempel: «Tegner vi alltid et rektangel når vi vet at to og to sider er like lange?» eller «Finnes det firkanter som har diagonaler som er like lange, som ikke er rektangler?».
Målet med diskusjonen er at elevene selv skal komme fram til at dersom alle vinkler er 90°, så er figuren et rektangel. Det betyr at alle firkanter med fire rette vinkler er rektangler. Denne egenskapen skal elevene ta utgangspunkt i når de skal tegne et rektangel i GeoGebra.
Oppgave 2 til elevene
- Slå av rutenettet og koordinatsystem.
- Tegn et rektangel som forblir et rektangel når du drar i hjørnene.
Kommentarer til læreren
Elevene skal de dra nytte av at et rektangel har fire rette vinkler. I dynamisk geometri skal en figur beholde formen uansett hvordan elevene snur og vender på den, for eksempel skal et rektangel være et rektangel selv om elevene drar i hjørnene. Dette kravet gjør det annerledes å tegne en geometrisk figur med dynamisk geometriprogram enn med papir og blyant.
Elevene skal slå av rutenettet og koordinatsystemet når de arbeider med geometri i GeoGebra. De har lov til å bruke alle verktøyknappene, og derfor sier vi at vi tegner, ikke at vi konstruerer. For at GeoGebra skal tolke en samling av linjestykker som en figur, må elevene bruke verktøyet Mangekant. Da får figuren navn og farge, i tillegg til at GeoGebra beregner arealet.
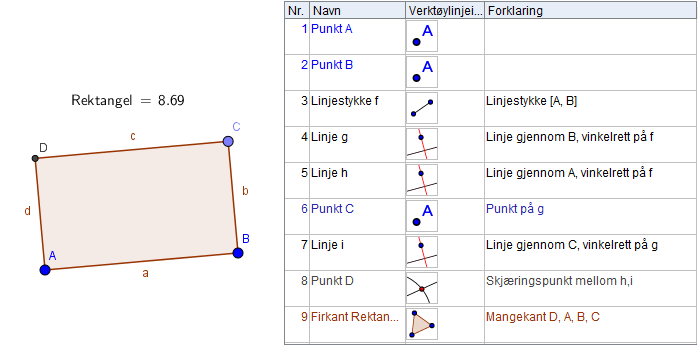
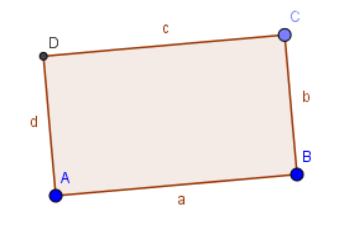
Forslag til hvordan elevene kan tegne et rektangel:
- Åpne GeoGebra og slå av rutenett og koordinatakser.
- Velg Linjestykke mellom to punkt for å lage et linjestykke. Dette gir punktene A og B og linjestykket f.
- Tegn Normal linje på endepunktene. Dette gir linjene g og h.
- Bruk Nytt punkt for å lage et punkt C som ligger fritt på linje g.
- Finn det fjerde punktet/hjørnet i rektangelet ved å tegne normalen gjennom punkt C på linje g (den får navnet linje i), og deretter lage Nytt punkt i skjæringspunktet mellom linjene h og i.
- Gjør rektangelet ferdig ved å bruke verktøyet Mangekant. Elevene kan med fordel gjøre linjestykke f og linjene g, h og i usynlig.
Elevene kan nå forsøke å dra i hjørnene for å endre på rektangelet. Da ser elevene at figuren forblir et rektangel selv om de drar i de blå hjørnene for å endre størrelse, form og plassering.
Selv om elevene har jobbet med rektangel som figur helt siden barnehagen, er begrepet «rektangel» ofte ikke godt utviklet hos mange elever. De kjenner til egenskapene, men har sjelden tenkt over at de har noe å si for en tegning. De færreste har tenkt over at to og to sider automatisk blir like lange og parallelle når alle vinkler er 90°. Det er viktig at elevene slår av rutenett og koordinatsystem når de jobber med geometri. Dersom de tegner alle figurer parallelt med rutenettet, kan det føre til en svak begrepsutvikling.
Aktivitet 2: Tegn et rektangel med omkrets 24
Oppgave 1 til elevene
- Bruk kvadratiske plastbrikker til å lage rektangler med omkrets 24.
- Noter løsningene i en tabell. Det er lurt å være systematisk.
- Se på tabellen. Skriv ned noen observasjoner.
Kommentarer til læreren
I denne aktiviteten er målet at elevene skal tegne et rektangel med en omkrets på 24 i GeoGebra. Aktiviteten starter med at elevene lager rektangler med omkrets 24 ved hjelp av kvadratiske plastbrikker. Elevene vil oppdage at det finnes mange løsninger, og de ser også at arealet endrer seg.
Forslag til tabell:
| Side1 | Side 2 | Areal |
|---|---|---|
| 1 | 11 | 11 |
| 2 | 10 | 20 |
| 3 | 9 | 27 |
| 4 | 8 | 32 |
| 5 | 7 | 35 |
| 6 | 6 | 36 |
| 7 | 5 | 34 |
| 8 | 4 | 32 |
| 9 | 3 | 27 |
| 10 | 2 | 20 |
| 11 | 1 | 11 |
Klassesamtale
I klassesamtalen studerer elevene og læreren resultatene i tabellen. Det er viktig at elevene oppdager at tabellen er symmetrisk, samt at summen av lengden og bredden alltid er 12 og at det er halvparten av omkretsen på 24. Læreren bør også forsikre seg om at elevene kjenner formelen for omkretsen til et rektangel. Deretter skal elevene og læreren sammen komme fram til sammenhengen mellom lengden, bredden og omkretsen til et rektangel.
Formelen for omkretsen til et rektangel er: o = 2a+2b
I dette tilfelle blir det 24 = 2a + 2b
Her har vi en likning med to ukjente, hvor de ukjente er avhengige av hverandre. Blir a større, må b bli mindre og omvendt. Hvis vi kjenner a, kan vi finne b:
b = `(24 - 2a)/(2)= 12 - a`
Elevene må bruke denne sammenhengen mellom a og b når de skal tegne figuren i GeoGebra.
Oppgave 2 til elevene
- Lag et rektangel med omkrets 24 i GeoGebra. Bruk metoden fra aktivitet 1, oppgave 2 og sammenhengen mellom side a og b i et rektangel med omkrets 24.
Kommentarer til læreren
Aktiviteten krever at elevene bruker kunnskaper om algebra. Mange elever ser ikke sammenhengen mellom ulike emner i matematikk, og det å bruke algebra for å lage en tegning i GeoGebra kan være helt nytt for dem. Ved å bruke algebra i varierte situasjoner, vil elevene få en dypere forståelse for emnet.
Elevene bruker først firkantbrikker til å lage rektangler med omkrets 24, og da finner de et endelig antall løsninger. Sidene har bare heltallsløsninger. I GeoGebra kan vi endre sidelengdene med små steg, noe som gir uendelig mange ulike rektangler med omkrets 24.
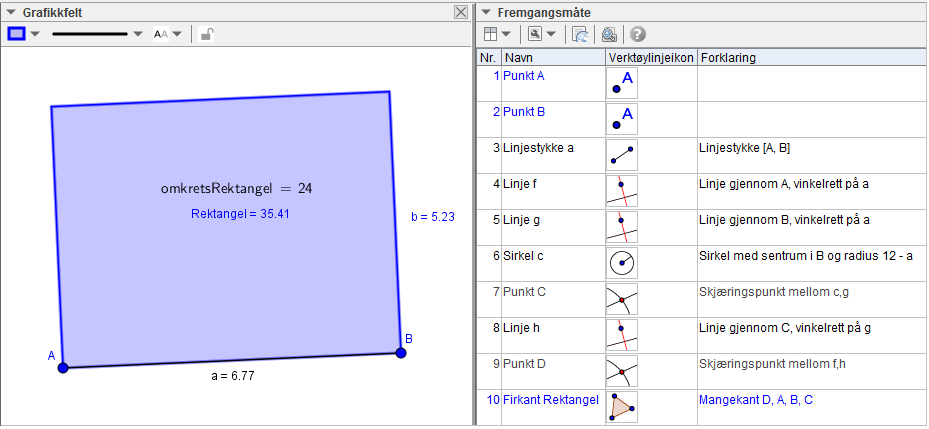
Forslag til hvordan elevene kan tegne et rektangel med omkrets 24 i GeoGebra:
- Åpne GeoGebra og slå av rutenett og koordinatakser.
- Tegn Linjestykke mellom to punkt og gi linjestykket navnet «a». Linjestykke a blir den første siden i rektangelet.
- Tegn Normale linjer på linje a i både punkt A og B. Linjene får navnene linje f og linje g.
- Side b i rektangelet ligger langs linje g (eller linje f). Lengden til side b avhenger av lengden til a, når omkretsen er bestemt. Velg Sirkel definert med sentrum og radius i punkt B for å finne ut hvor lang side b skal være.

- Skriv inn høyre delen av formelen for b (lengden av b, gitt a).
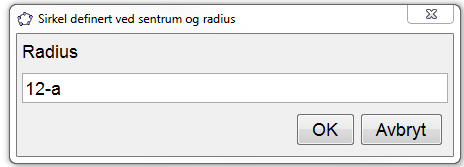
- Marker skjæringspunktene, og tegn rektangelet med Mangekant.
- Vis omkretsen og arealet til rektangelet. Omkretsen finner du ved å velge Avstand eller lengde og klikke i mangekanten. Arealet finner du ved å vise «Verdi» for mangekanten.
- Legg merke til at rektangelet bare har to blå punkter (punkter som elevene kan dra i). Det kommer av at bredden er avhengig av lengden (når elevene endrer på a, endrer b seg).
- Lagre figuren.
Elevene kan teste svarene de fikk i tabellen ved å dra i ett av de blå punktene. Finn rektangelet med det største arealet. Hvor lange er sidene da?
Aktivitet 3: Tegn arealet som en funksjon
Oppgave 1 til elevene
- Finn en funksjon for arealet til et rektangel med omkrets 24. Gi den navnet R(x).
- Jobb videre med GeoGebra-fil fra aktivitet 2.
- Åpne Grafikkfelt 2 og klikk i feltet.
- Skriv funksjonen i Skrivefeltet. GeoGebra viser grafen i Grafikkfelt 2.
- Hva kaller vi en graf med denne formen?
- Koble sammen Grafikkfelt og Grafikkfelt 2 ved å skrive x = «navnet på lengden i rektangelet ditt» i Skrivefeltet.
- Finn skjæringspunktet mellom grafen og linjen.
- Hva forteller koordinatene til skjæringspunktet?
Klassesamtale
I helklassesamtale skal elevene forklare sammenhengen mellom de to vinduene (tegningen av rektangelet og grafen). Læreren må stille gode spørsmål som inviterer til tenking, for eksempel:
- Hva skjer med punktet på grafen når vi endrer lengden til rektangelet?
- Hva viser grafen?
- Hvor finner vi verdien av x-aksen i rektangelet?
- Hva betyr verdiene på y-aksen? Hvor finner vi dem i rektanglet?
- Hva betyr det at grafen er en parabel?
- Finn rektanglet med størst areal. Hvordan ser det ut?
- Hvorfor er det lurt å avgrense grafen til x-verdier mellom 0 og 12?
Kommentarer til læreren
Elevene skal bruke resultatene fra aktivitet 1 og 2 til å lage en funksjon som viser sammenhengen mellom arealet og omkretsen til rektangelet. Omkretsen til rektangelet er fortsatt 24. Elevene kjenner formelen for arealet til et rektangel og formelen for side b når omkretsen er 24. Ved å kombinere de to får elevene en formel for arealet til rektangelet som avhenger av lengden til side a.
Formelen for arealet til et rektangel: A = a∙b
Formelen for side b når omkretsen er 24:
b = `(24-2a)/(2) = 12-a`
Ved å sette inn uttrykket for b i formelen for A får elevene: A = `a(24 - 2a)/(2) = a(12-a)`
Denne formelen kan elevene tegne i GeoGebra, men siden bokstaven A allerede er brukt i GeoGebra-filen, må funksjonen få et nytt navn, for eksempel R(x).
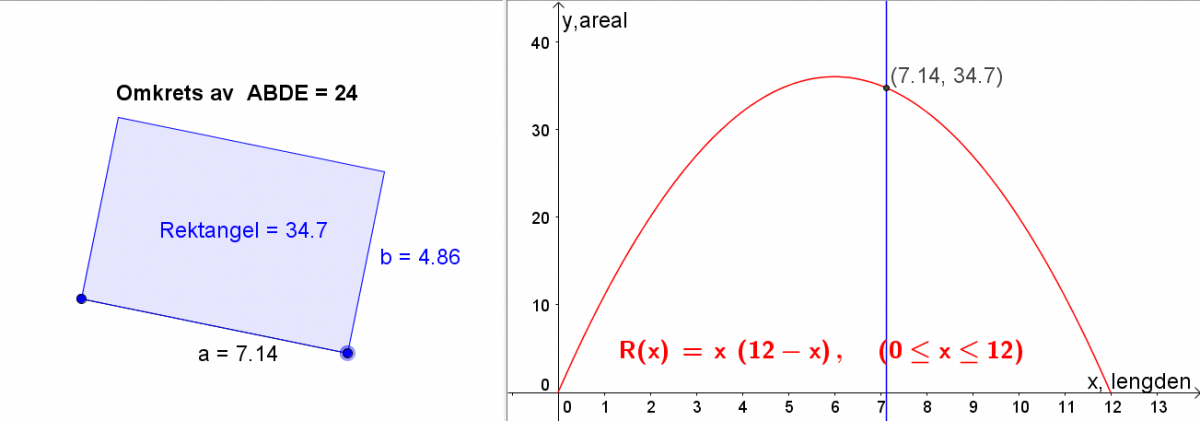
Elevene får da følgende funksjon for arealet til et rektangel med omkrets 24: R(x) = x(12 - x)
Dette er en fin anledning til å synliggjøre at dette er en kontinuerlig funksjon, i motsetning til tabellen med brikkene der funksjonen bare er definert for naturlige tall mellom 1 og 24.
Forslag til fremgangsmåte i GeoGebra:
- Åpne filen med rektangelet med omkrets 24.
- Åpne Grafikkfelt 2 og klikk i grafikkfeltet for å aktivere det.
- Skriv funksjonen R(x) inn i Skrivefeltet og Grafikkfelt 2 viser funksjonen.
Hvis den vises i Grafikkfelt, er Grafikkfelt 2 ikke aktivert. Slett funksjonen og prøv på nytt.
- Aktiver Grafikkfelt 2 og skriv x = a. GeoGebra tegner en loddrett linje.
- Finn skjæringspunktet mellom grafen og linjen. Gjør koordinatene synlige.
Elevene må skrive x = a for å binde Grafikkfelt og Grafikkfelt 2 sammen. Det betyr at alle x-verdiene i Grafikkfelt 2 blir erstattet med verdien som a representerer (a er lengden av siden AB). På denne måten vil x-verdien i Grafikkfelt 2 endre seg når elevene endrer sidelengden i rektangelet.
Aktiviteten lærer elevene å se sammenhengen mellom en graf og en geometrisk figur, og algebra er nødvendig for å klare å tegne figuren. Sammenhengen er dynamisk i den forstand at arealet til rektangelet endrer seg når vi flytter punktet på grafen. Årsaken er at ligningen x = a binder de to vinduene sammen, altså at x-koordinaten i Grafikkfelt 2 har samme verdi som lengden på linjestykke a i Grafikkfelt. Opplegget viser at praktisk bruk av algebra gir mening, noe som kan øke elevenes motivasjon for å lære et emne som mange oppfatter som veldig teoretisk.
GeoGebra er kresen når det gjelder valg av bokstaver. Elevene kan ikke bruke den samme bokstaven som navn på ulike elementer. Det krever en nøyaktighet fra elevene som de ikke alltid er vant med, men som er viktig for senere læring.
Utvidelse av oppgaven
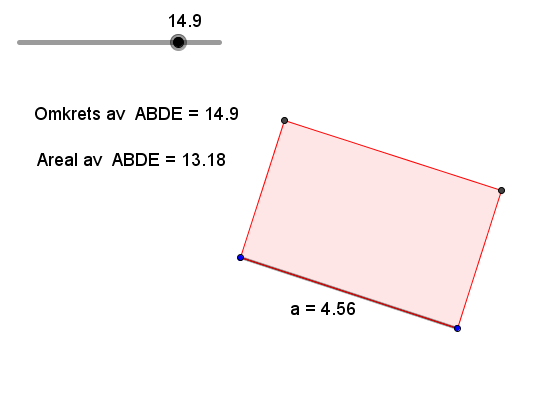
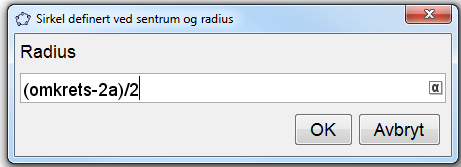
I dette opplegget er omkretsen 24, men det er også mulig å variere omkretsen. Da må elevene lage en Glider som de kan kalle for «omkrets», og så må de erstatte «24» i formlene med ordet «omkrets».
Tips til alternativt undervisningsopplegg
Dette undervisningsopplegget ser på sammenhengen mellom geometri, algebra og funksjoner. Dersom dere kun ønsker å se på sammenhengen mellom geometri og algebra, kan dere se på dette undervisningsopplegget: Rektangel med omkrets 24.
Rammeplanmål/Kompetansemål
- Videregående
- R1
- bruke ulike strategier for å utforske og bestemme grenseverdier til funksjoner, og utforske og argumentere for anvendelser av grenseverdier
- S1
- bruke ulike strategier for å utforske og bestemme grenseverdier til funksjoner, og utforske og argumentere for anvendelser av grenseverdier
- forstå begrepene gjennomsnittlig og momentan vekstfart, grenseverdi og derivasjon, og bruke disse for å løse praktiske problemer
- Vg1P
- bruke digitale verktøy i utforsking og problemløysing knytt til eigenskapar ved funksjonar, og diskutere løysingane
- identifisere variable storleikar i ulike situasjonar og bruke dei til utforsking og generalisering
- tolke og bruke formlar som gjeld samfunnsliv og arbeidsliv
- tolke og bruke funksjonar i matematisk modellering og problemløysing
- Vg1T
- identifisere variable storleikar i ulike situasjonar, setje opp formlar og utforske desse ved hjelp av digitale verktøy
- Vg2P
- utforske og forklare korleis formlikskap, målestokk og eigenskapar ved geometriske figurar kan brukast i berekningar og i praktisk arbeid