Utforske andregradsfunksjoner 1
Emne
Funksjoner, andregradsfunksjoner, ekstremalpunkt, nullpunkt, fullstendig kvadrat, GeoGebra
Hensikt
Målet er å lære elevene om fordelene til ulike måter å skrive funksjonsuttrykket til andregradsfunksjoner på.
Valg av tidspunkt
Du trenger
Aktiviteten
I dette opplegget skal elevene utforske ulike skrivemåter for andregradsfunksjoner. De skal se på funksjoner fremstilt på følgende måter:
`f(x)=ax^(2)+bx+c`
`g(x)=k(x-r)(x-s)`
`h(x)=t(x-m)^(2)+n`
Når elevene skal skrive uttrykket til en andregradsfunksjon, vil de som regel notere funksjonen på formen til f(x) siden det er den formen de har arbeidet mest med og som lærebøker bruker oftest. I dette opplegget skal elevene bli bedre kjent med alle skrivemåtene og fordelene til hver av dem.
Hvert elevpar får ett elevark for aktivitet 1, 2 og 3 og ett elevark for aktivitet 4 og 5, Vi anbefaler at elevene får arket med aktivitet 4 og 5 etter at de har jobbet med aktivitet 1, 2 og 3. Elevene skal forklare tankene sine for hverandre og samarbeide om å skrive ned observasjonene sine. Vi foreslår at elevene jobber sammen på en PC, men bytter på å skrive inn i GeoGebra.
For alle oppgaver gjelder:
- Lag en ny fil i GeoGebra for hver aktivitet
- Skriv funksjonen inn i GeoGebra. Lag glidere. Vis Navn og verdi på alle Glidere.
- Undersøk bare en parameter (glider) om gangen.
- Observer og noter observasjonene.
- Sett alltid glidere tilbake til startverdien før du starter på en ny parameter.
Elevene arbeider i eget tempo med aktivitetene, og vi anbefaler å notere ned hva elevene synes er vanskelig underveis og diskutere det i oppsummeringen. Hvis noen elever jobber lenge med en aktivitet og ikke kommer fram til en god løsning, kan det være lurt at de går videre til neste aktivitet slik at de kan få en viss oversikt over hele opplegget.
Aktivitet 1
Elevene skal undersøke `f(x)=ax^(2)+bx+c`.
- Sett alle glidere på tallet 1,5 (NB:1.5 i GeoGebra).
- Undersøk c, a og b (tabell på elevark).
Kommentarer til læreren
GeoGebra setter startverdien for glidere på 1. Tallet 1 er et spesialtilfelle som lett kan gjøre at elevene feiltolker egenskapene til et funksjonsuttrykk. Elevene skal derfor bruke 1,5, som er et vilkårlig valgt tall, som utgangspunkt for undersøkelsene.
Rekkefølgen til parameterne som elevene skal undersøke er satt til c, a, b. Egenskapene til parameter c og a skal være kjent for elevene. Parameter c er den enkleste å finne ut av. Egenskapene til parameter b er ukjent for elevene. Som hjelp blir de bedt om å tegne inn Ekstremalpunkt og sette sporing på den. Elevene finner ekstremalpunktet ved å skrive inn Ekstremalpunkt i skrivefeltet eller ved å velge Ekstremalpunkt fra verktøylinjen.
Elevene blir bedt om å undersøke tilfellene der parameterne er lik 0. De blir ofte overrasket over at grafen blir en rett linje når a = 0. Det er først da mange elever ser en sammenheng mellom lineære funksjoner og andregradsfunksjoner, noe som kan gi dem en dypere forståelse for funksjoner.
Aktivitet 2
Elevene skal undersøke `g(x)=k(x-r)(x-s)`.
- Sett glidere til: k = 1, s = -4, r = 2.
- Undersøk parameter k. Hva skjer med grafen når k er positiv, negativ, 1 eller 0? Legg merke til både det som endrer seg og det som ikke endrer seg.
- Hvor på grafen finner dere s og r?
- Flytt s og r etter tur. Hva skjer med grafen?
- Hva kaller vi slike punkter?
- Noter med egne ord hva som dere kan lese ut av funksjonen: `p(x)=-1,5(x-3)(x-4)`
- Kontroller svaret med GeoGebra. Skriv eventuelt et nytt svar.
Kommentarer til læreren
Eleven starter med å undersøke parameter k. Da vil de se at grafen henger fast på to punkter på x-aksen. Mange elever vil gjenkjenne disse punktene som nullpunkter. De fleste elevene vil også se at parameter k påvirker grafen på samme måte som parameter a i aktivitet 1. Det vil si at funksjonen har et bunnpunkt hvis k er positiv og et toppunkt hvis k er negativ. Spesielt interessant er tilfellet der k = 0. Da ligger grafen på x-aksen.
Så skal elevene undersøke r og s. Det kan være overraskende for elevene å se at skjæringspunktene med x-aksen beveger på seg. Parameterne r og s betegner x-koordinatene til nullpunktene til funksjonen. Dersom elevene tror at r og s bestemmer formen til grafen, kan det være lurt å be de om å bruke verktøyet Skjæring mellom to objekt og vise verdi på punktene.
Til slutt skal elevene anvende det de har funnet ut på en gitt andregradsfunksjon. Det viser om elevene har forstått hva parameterne betyr. For elevene kan det være en utfordring å tolke operasjonstegnene i parentesene riktig. (x-3) betyr at funksjonen har et nullpunkt ved x = 3. Gjennom utforsking kan de se at y-koordinaten alltid er 0 for alle punkter på x-aksen.
Aktivitet 3
Elevene skal undersøke `h(x)=t(x-m)^(2)+n`.
- Sett gliderne på 1,5.
- Utforsk t, m og n (tabell på elevark).
- Tegn et punkt med koordinater P = (m, n).
- Hvor ligger dette punktet?
- Hva heter punktet?
- Finn nullpunktene til h(x).
- Tegn linja x = m. Hva heter denne linja?
- Flytt på gliderne og noter observasjonene deres.
Kommentar til læreren
Denne måten å skrive uttrykket til en andregradsfunksjon er ukjent for elevene. Elever som har hatt 1T har brukt skrivemåten som en løsningsmetode for andregradslikninger (fullstendig kvadraters metode), men elevene har aldri sett den i sammenheng med funksjoner. Elevene ser her at noe som er kjent fra algebra gir verdifulle opplysninger i funksjonslære, noe som kan gi dem dypere forståelse i matematikk.
Aktiviteten er tredelt. Elevene arbeider først med parameterne t, m og n. De vil oppdage at t bestemmer om funksjonen har en minimal- eller maksimalverdi, men at den ikke endrer på koordinatene til ekstremalpunktet. Ved å endre m og n, kan elevene flytte grafen langs x- og y-aksen, og dermed endre grafens ekstremalpunkt.
I andre del av aktiviteten blir elevene bedt om å skrive inn punkt P = (m, n). De fleste elevene vil da oppdage at m og n er koordinatene til ekstremalpunktet til funksjonen h.
Til slutt skal elevene undersøke sammenhengen mellom funksjonens nullpunkter, ekstremalpunkt og symmetrilinje. Målet er at elevene skal oppdage at x-verdien til ekstremalpunktet alltid er midt i mellom x-verdiene til nullpunktene og at symmetrilinja går gjennom ekstremalpunktet. Dette kan elevene utnytte når de skal skissere grafen til en andregradsfunksjon uten å lage verditabell.
Aktivitet 4
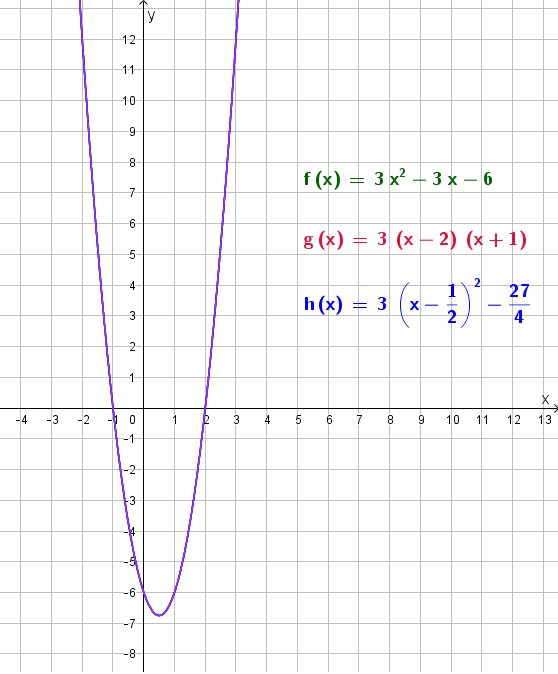
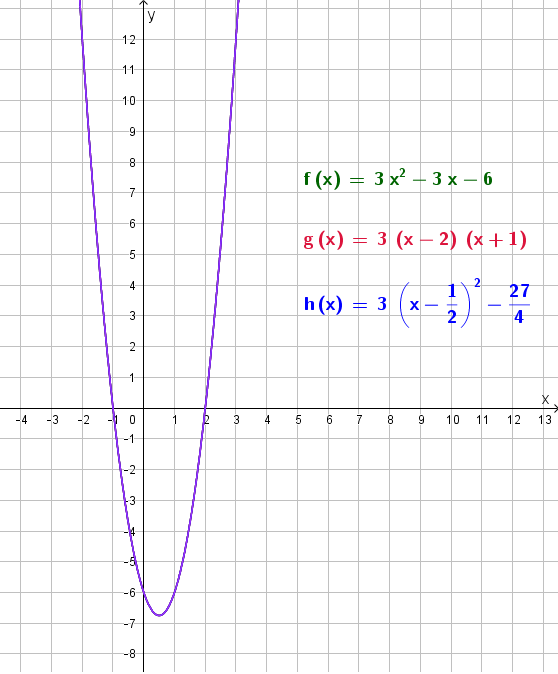
Elevene skal undersøke en funksjon F som er skrevet på tre forskjellige måter.
`f(x)=3x^(2)-3x-6`
`g(x)=3(x-2)(x+1)`
`h(x)=3(x-(1)/(2))^(2)-(27)/(4)`
- Finn ut mest mulig om grafen uten hjelpemidler (tabell på elevark).
- Vis ved regning at f(x) = g(x) = h(x).
Kommentar til læreren
I denne aktiviteten skal elevene oppsummere hva de har funnet ut i aktivitet 1-3. Det er anbefalt at hver elevgruppe bare får ett elevark slik at de er nødt til å jobbe sammen og diskutere for å komme fram til et svar.
Elevene skal se at alle skrivemåtene har sine fordeler, og at det er mulig å skifte mellom de ulike skrivemåtene. Det gjør det mulig å skissere grafer uten digitale hjelpemidler, noe elevene får prøve når de skal skissere i(x) i aktivitet 5. Elevene skal notere ned hvilken funksjon de bruker for å finne de forskjellige verdiene/egenskapene, og det gjør de mer bevisste på fordelene de ulike skrivemåtene har.
For å vise at f(x) = g(x) = h(x), må elevene bruke algebra. Det er ikke nok å tegne grafen til funksjonene og vise at de dekker hverandre. Det er enklest å omskrive uttrykkene til g(x) og h(x) til f(x). Elever som trenger utfordringer kan omforme f(x) til h(x).
Det er viktig å ha god tid til en grundig, felles oppsummering etter aktivitet 4. Læreren bør ha fokus på å få fram hva elevene har funnet ut og hvilke fordeler de ulike skrivemåtene har når elevene arbeider med funksjoner. Det er viktig å løfte frem hvordan elevene kan dra nytte av fordelene når de skal skissere en graf.
Aktivitet 5
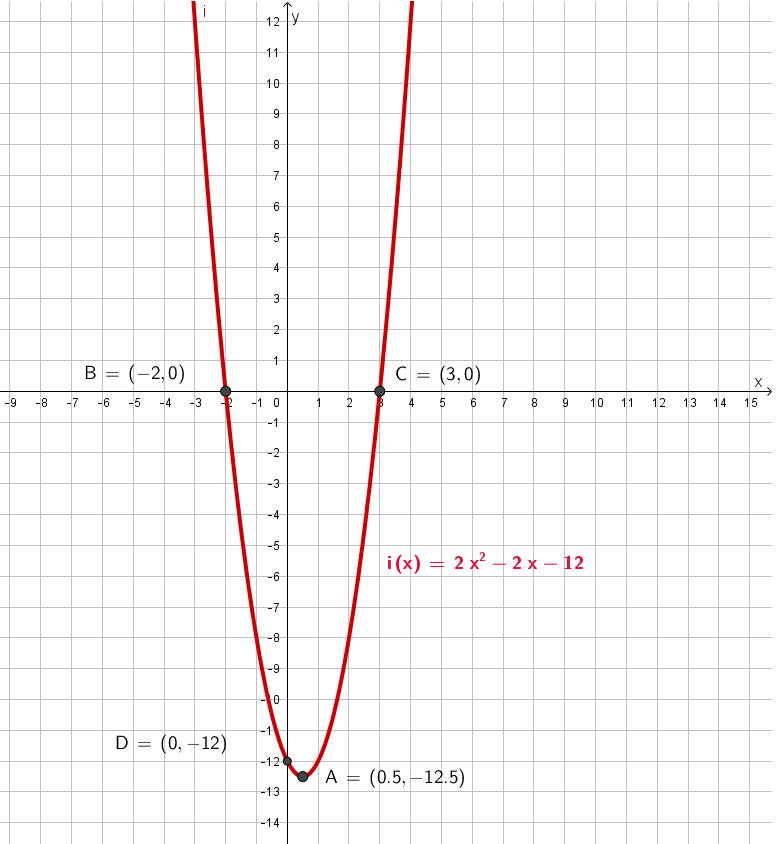
Elevene skal skissere funksjonen `i(x)=2x^(2)-2x-12` i koordinatsystemet uten bruk av hjelpemidler og uten å regne ut en verditabell.
Kommentarer til læreren
Tallene er valgt slik at det skal være lett å veksle mellom de tre skrivemåtene.
Elevene skal bruke det de har lært i aktivitetene 1- 4 for å skissere grafen. De fleste elevene vil se at grafen skjærer y-aksen i punktet (0, -12). Det kan de lese direkte ut av det oppgitte uttrykket til i(x). Elevene kan finne nullpunktene ved å faktorisere uttrykket slik at det blir på formen til g(x) eller ved å sette i(x) = 0 og løse likningen. For å finne ekstremalpunktet, vil noen elever benytte seg av at x-verdien til ekstremalpunktet må ligge midt i mellom nullpunktene siden en andregradsfunksjon er symmetrisk, og deretter kan de beregne y-verdien ved å sette inn i uttrykket for i(x). Andre elever vil fullføre kvadratet og bruke det de har lært i aktivitet 3 og 4.
I oppsummeringen etter aktivitet 5 skal elevene fortelle hvordan de arbeidet og hvordan de utnyttet fordelene til funksjonsuttrykkene. Dette kan skje i hel klasse hvor læreren velger ut noen elevpar som forteller, eller det kan skje i grupper bestående av flere elevpar.
GeoGebra-hjelp
Glidere
Noen av oppgavene forutsetter bruk av Glidere. Den enkleste måten å lage disse på, er å skrive inn funksjonen slik den står og svare bekreftende på spørsmål om glidere. Minn elevene på at de må bruke gangetegn mellom to bokstaver slik som a og x2 og b og x.
Mange elever vil oppleve at gliderne er i veien for grafen. De kan flytte gliderne ved å høyreklikke og ta bort haken ved Lås objekt.
Rammeplanmål/Kompetansemål
- Videregående
- R1
- analysere og tolke ulike funksjoner ved å bruke derivasjon
- bestemme den deriverte i et punkt geometrisk, algebraisk og ved numeriske metoder, og gi eksempler på funksjoner som ikke er deriverbare i gitte punkter
- forstå begrepene vekstfart, grenseverdi, derivasjon og kontinuitet, og bruke disse for å løse praktiske problemer
- S1
- anvende derivasjon til å analysere og tolke egne matematiske modeller av reelle datasett
- forstå begrepene gjennomsnittlig og momentan vekstfart, grenseverdi og derivasjon, og bruke disse for å løse praktiske problemer
- uttrykke egne resonnementer ved hjelp av matematiske begreper og symbolspråk
- Vg1T
- forklare polynomdivisjon og bruke det til å omskrive algebraiske uttrykk, drøftedrøfte funksjonar og løyse likningar og ulikskapar
- utforske og beskrive eigenskapane ved polynomfunksjonar, rasjonale funksjonar, eksponentialfunksjonar og potensfunksjonar
- utforske samanhengar mellom andregradslikningar og andregradsulikskapar, andregradsfunksjonar og kvadratsetningane og bruke samanhengane i problemløysing
- Vg2P
- utforske strategiar for å løyse likningar, likningssystem og ulikskapar og argumentere for tenkjemåtane sine