Hva er MAM?
Modellen er utviklet ved Matematikksenteret i samarbeid med forskere fra University of Washington. Ressursene er forskningsbaserte og tilrettelagt for norske forhold i tett samarbeid med praksisfeltet. Det matematiske innholdet er knyttet til tallforståelse.
Modellen består av en syklus med seks komponenter som kan benyttes både for studenter i praksis, lærere i etter- eller videreutdanning eller av en gruppe lærere som vil drive kompetanseutvikling sammen.
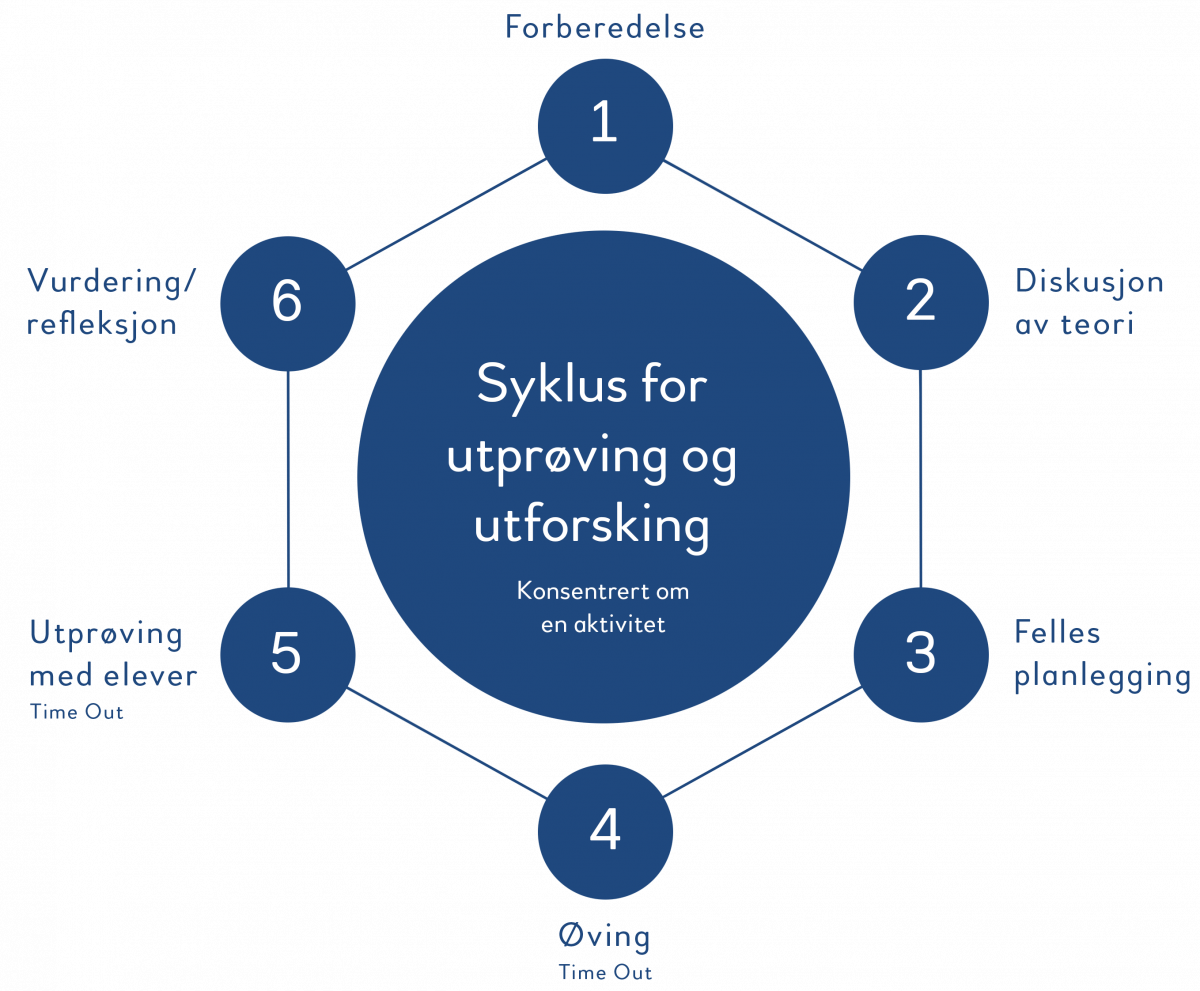
Beskrivelse av komponentene
- Deltakerne leser en artikkel med teori knyttet til det aktuelle temaet i syklusen.
Observasjon: deltakerne observerer enten en filmet undervisningssekvens eller en veileder/lærerutdanner som gjennomfører en aktivitet med elevene. - Veileder/lærerutdanner leder en diskusjon mellom deltakerne. Hva fra punkt 1 kan vi ta med oss inn i planleggingen av undervisningsøkta?
- Deltakerne planlegger sammen ei undervisningsøkt med samme type aktivitet som i punkt 1. Gruppestørrelse 6-10. Veilederne/lærerutdannerne er aktive deltakere i sin gruppe uten å overta arbeidet for deltakerne. Gruppen lager et felles undervisningsnotat som viser gangen i økta med elevene.
- Deltakerne øver på aktiviteten i gruppa. En eller to av deltakerne har rollen som lærer, resten av deltakerne er «elever». Alle deltakerne og veilederen/lærerutdanneren kan be om Time-Out. Da tar man et kort avbrekk og diskuterer hva man bør gjøre.
- Aktiviteten blir prøvd ut med en elevgruppe. Time-Out kan brukes også under utprøvingen.
- Diskusjon om utprøvingen i gruppa. Både deltakere, veilederen/lærerutdanneren deltar.
Ressursene som er utviklet gjennom MAM-prosjektet er samlet i ti moduler til bruk i nettverk mellom skoler eller skolebasert utviklingsarbeid med støtte fra eksterne fagmiljø.
Gjennom arbeidet med de ti modulene blir deltakerne introdusert for fem ulike undervisningsaktiviteter. Hver av modulene er sentrert om en av aktivitetene. Til støtte i arbeidet med modulene er det i tillegg til artikler og fagtekster utviklet flere ressurser til hver av de fem aktivitetene syklusene er konsentrert om.
Aktivitetene er designet for å støtte lærerne i arbeidet med å lære prinsippene og kjernepraksisene i ambisiøs matematikkundervisning. Aktivitetene legger forholdene til rette for produktive matematiske samtaler i klasserommet, arbeid med sentrale matematiske ideer og bruk av ulike representasjoner. Ved å bruke disse aktivitetene reduserer man kompleksiteten i arbeidet med å lære seg ambisiøs matematikkundervisning.
Ressurser til modulene
Aktivitetene
Arbeidet med å mestre ambisiøs matematikkundervisning tar utgangspunkt i fem undervisningsaktiviteter som er utviklet spesielt med tanke på lærernes utvikling av ambisiøs matematikkundervisning: Kvikkbilder, Telle i kor, Oppgavestrenger, Spill og Problemløsing. Aktivitetene kan betraktes som "bærere" av viktige prinsipper og praksiser.
Kort beskrivelse av aktivitetene.
Kvikkbilder
Aktiviteten Kvikkbilde er designet for å engasjere elever i å forme mentale representasjoner av en mengde, for eksempel fire grupper av fem prikker. Elevene blir oppfordret til å bruke effektive strategier for å finne ut hvor mange objekter det er, i stedet for å telle ett og ett. Kvikkbildet kan være et fotografi, en tegning, tier-rammer, klistremerker arrangert på et ark eller magneter på en magnettavle.
Telle i kor
Telle i kor er en aktivitet hvor klassen teller sammen ved å legge til eller trekke fra et bestemt tall, mens læreren skriver det elevene teller på tavlen. Læreren stopper tellingen ved strategiske punkter, slik at elevene kan beskrive og begrunne mønster som kommer fram og bruke mønstrene når de fortsetter å telle.
Oppgavestrenger
En oppgavestreng er en sekvens med 4-6 relaterte regnestykker som er designet for å engasjere elever i en diskusjon om en bestemt strategi i arbeid med for eksempel multiplikasjon eller andre regneoperasjoner. Aktiviteten kan også brukes for å diskutere egenskaper ved regneoperasjoner.
Spill
Spillene som er valgt ut gir læreren muligheter til å løfte fram sentrale matematiske ideer. I tillegg vil elevene også kunne få verdifull ferdighetstrening i de fire regneartene. Kreativitet og strategisk tenking er andre aspekter ved matematisk aktivitet som kan fremmes gjennom spill.
Problemløsing
Her defineres et problem som «en oppgave der eleven ikke umiddelbart ser hvordan han kan komme videre i løsningsprosessen, og ingen kjent løsningsmetode kan brukes». Formålet med denne aktiviteten er først og fremst å sette søkelyset på strategier for matematisk problemløsing. Til det formålet introduseres oppgaver som naturlig vil lede til den strategien som skal fremmes.
Plandokumenter
Til enkelte aktiviteter er det utarbeidet plandokumenter som viser hvordan prosjektgruppa har arbeidet med å planlegge og gjennomføre aktivitetene. Videre finnes det maler med sentrale punkter læreren må ta hensyn til under planleggingen. Det er også utviklet maler for kortere undervisningsnotat som læreren kan bruke i planleggingen og utprøvingen av en aktivitet.
Filmer med transkripsjoner og diskusjonsspørsmål
Til hver av aktivitetene er det laget en eller flere filmer som viser hvordan aktivitetene kan gjennomføres med elever. Filmene er ikke eksempler på eksemplarisk undervisning. Tanken er at de kan brukes som observasjon i forberedelsen til arbeidet med en modul. Til hver film er det utarbeidet en transkripsjon og diskusjonsspørsmål.
Artikler og fagtekster
Artiklene og fagtekstene bidrar til å gi lærere en grundigere innføring i aktivitetens potensiale og det matematikkdidaktiske grunnlaget ambisiøs matematikkundervisning bygger på.
Bakgrunn
Gjennom prosjektet «Mestre Ambisiøs Matematikkundervisning» (MAM, 2015-2018), utviklet Matematikksenteret ressurser til bruk i en modell for skolebasert etterutdanning knyttet til ambisiøs matematikkundervisning. Se mer om bakgrunnen for MAM i prosjektbeskrivelsen. Prosjektbeskrivelsen har referanser til den forskningen MAM-modellen for kompetanseutvikling bygger på.