Lag det tallet

Vurdere tallstørrelser og forståelse for hva de ulike regneoperasjonene gjør med tallene.
Eksperimentering med tall og øvelse i hoderegning.

Dette opplegget er utviklet som en del av MAM-prosjektet. 

Kortstokk. Skrivesaker og papir. Tavle.

Spillets gang:

1. Del ut fem kort til hver elev.
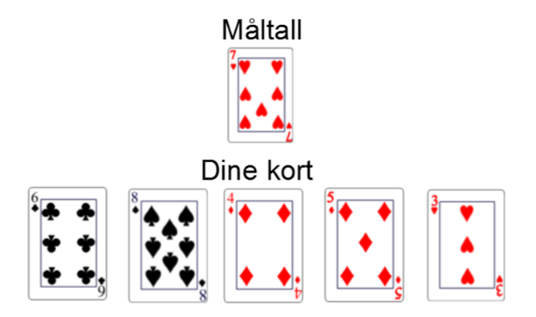
2. Snu det øverste kortet i bunken med bildesiden opp. Dette er måltallet.
3. Hver spiller prøver å kombinere sine kort ved addisjon/subtraksjon/multiplikasjon og divisjon for å lage måltallet. De kan bruke så mange av de fem kortene som de ønsker, men hvert kort kan brukes bare en gang.
4. Hver spiller skriver sitt beste forslag på et ark og legger til side kortene de har brukt.
5. Kortet med måltallet legges i bunnen av kortstokken.
6. Spillerne tar nye kort, like mange som han/hun har brukt til å lage regnestykket.
7. Nytt kort fra toppen av kortstokken snus og blir det nye måltallet. Ny runde spilles.
8. Spillet fortsetter til det ikke er flere kort å trekke for å erstatte kort som spillerne har spilt ut.
9. Vinneren er den som har spilt ut flest kort, dvs. brukt flest kort på å danne måltallet.
10. Klassesamtale som oppsummerer noen aspekter ved aktiviteten

Eksempel: Måltallet er 8 og kortene man trekker er 9 – 5 – 3 – 6 – 4.
Mulige løsninger kan være: 5 + (6 – 3) (bruker 3 kort), eller (9 – 3) + (6 – 4) (bruker 4 kort), eller (9 + 3 – 4) · (6 – 5) (bruker alle 5 kortene).

Matematiske sammenhenger

I dette spillet skal elevene kombinere ulike tall for å lage måltallet. Elevene kan bruke alle regnearter og kombinere tallene slik at de oppnår ønsket måltall. De kan bruke to eller flere kort for å lage tallet. Det er selvfølgelig lurt å bruke så mange kort som mulig, da vinneren er den som bruker flest kort. Elevene skriver regnestykket som gir måltallet i hver runde. Dette utfordrer elevene på hvordan de så presist som mulig, kan vise utregningen de gjør. I klassesamtalen om spillet, kan du som lærer legge vekt på ulike ting.

Vi har valgt å legge fokus på fire ulike matematiske sammenhenger du kan trekke fram i samtalen med elevene. Disse sammenhengene er: effektive hoderegningsstrategier, prioritering av regnearter, matematisk notasjon og bruk av identitetselement.

Strategier

Når elevene får sine kort kan de tilfeldig begynne å prøve ulike kombinasjoner med kortene sine. Etter litt prøving og feiling kan de finne fram til kombinasjoner som gir måltallet. En mer effektiv strategi kan være å se på måltallet, vurdere hvilke tallkombinasjoner som gir dette tallet og se om man kan lage disse tallkombinasjonene. 

Vi ser på et eksempel der måltallet er 8. Eleven vurderer hvilke kombinasjoner som gir 8, f.eks. 0 + 8, 1 + 7, 2 + 6 osv. 9 – 1, 10 – 2, 11 – 3 osv.  2 · 4 eller 16 : 2 osv. En annen måte kan være å ta utgangspunkt i et tall de kan lage for eksempel 5. De tenker videre hva må jeg gjøre med 5 for å få 8. Elevene kan også ta utgangspunkt i to kort de har, f.eks. 9 og 3. De vurdere hvilke tall de kan lage med disse tallene. De kan addere, 9 + 3 = 12, subtrahere, 9 – 3 = 6, multiplisere, 9 · 3 = 27 eller dividere, 9 : 3 = 3.

Prioritering av regnearter, bruk av likhetstegnet og matematisk notasjon

Å prioritere regnearter i riktig rekkefølge er vanskelig for mange elever og det er ikke så enkelt å finne gode situasjoner som viser konsekvensen av reglene for prioritering av regnearter.  I denne aktiviteten kan det være mulig å finne gode eksempler på hvordan prioritering av regneartene slår ut ved å prioritere ulikt.

Det er kort vei fra prioritering av regnearter til matematisk notasjon med parenteser. Vi kan se på diskusjon om prioritering av regnearter, som et steg på veien til å se behovet for parenteser. En elev laget måltallet 8 med følgende regnestykke: 13 – 11 · 3 + 2 · 1. Følger man reglene for prioritering av regnearter får man (– 18) som svar. Dette eksemplet viser hvorfor man må bruke parenteser for å beskrive de ulike regneoperasjonene eleven har gjort. Med bruk av parenteser ser regnestykket slik ut: ((13 – 11) · 3 + 2) · 1.

I sammenheng med diskusjon om prioritering av regnearter, vil behovet for å bruke parenteser naturlig tvinge seg frem. Når elevene oppdager denne muligheten, vil det helt sikkert komme mange fine eksempler som kan brukes i oppsummering av spillaktiviteten. Velg ut eksempler som viser bruk av parenteser på ulike måter, både nødvendig/unødvendig og riktig/gal bruk av parenteser.

Elever har ofte en ukritisk bruk av = - tegnet. F.eks. 2 + 3 = 5 · 4 = 20 – 8 = 12 : 2 = 6. Slike regnestykker vil være et godt utgangspunkt for å diskutere bruk av likhetstegnet.

I stedet for å bruke likhetstegnet, kan piler brukes for å beskrive stegene i tenkingen: 
2 + 3 → 5 · 4 → 20 – 8 → 12 : 2 → 6. Bruk av piler er et steg på vegen mot å se flere operasjoner i et og samme uttrykk, gjerne ved bruk av parenteser. Dette vil være sentralt for å kunne diskutere egenskaper ved multiplikasjon.

Bruk av identitetselementer

0 er identitetselement ved addisjon og subtraksjon og 1 er identitetselement ved multiplikasjon og divisjon. Målet med spillet er å bruke flest mulig kort. Å utnytte identitetselement vil være en effektiv måte å få brukt flere kort uten at de har betydning for svaret på regnestykket. Dersom man velger å framheve denne strategien, velg eksempler som viser hvordan man kan utnytte identitetselementer i addisjon/subtraksjon og multiplikasjon/divisjon. Identitetselementene utnyttes både i brøkregning og arbeid med ligninger. I brøkregning utnyttes identitetselementet 1 når vi finner fellesnevner og ved utvidelse og forkortelse av brøker. Vi multipliserer eller dividerer med 1 og skriver 1 som brøk på en slik måte at vi får fine tall å jobbe med. I arbeid med ligninger utnytter vi identitetselementene når vi jobber for å få x alene på den ene siden av likhetstegnet.