Småkaker i kakeboksen

Problemløsingsstrategier. Egenskaper ved brøk.

Opplegget er utviklet i forbindelse med MAM (Mestre Ambisiøs Matematikkundervisning)

Papir og skrivesaker.

Plastbrikker.

Til lærer

Oppgaveark Småkaker i kakeboksen [PDF]

Observasjonsskjema Småkaker i kakeboksen [PDF]

Kort undervisningsnotat problemløsing [PDF]

Presenter oppgaven som en fortelling (muntlig) for elevene. La gruppene diskutere og komme med forslag i plenum om hvordan de vil starte arbeidet med problemet. Når elevene starter arbeidet med problemet, får de utdelt oppgaven skriftlig i tillegg til plastbrikker de kan bruke om de ønsker det.

Elevene får i oppgave å finne ut hvor mange småkaker det var i kakeboksen til bestemor og bestefar før barnebarna begynte å forsyne seg. Elevene arbeider i grupper og kommer med forslag, som også skal uttrykkes skriftlig. Læreren observerer arbeidet og velger rekkefølgen på presentasjonene.

Under oppsummeringen presenterer gruppene sine forslag, og læreren noterer på tavla. Elevene beskriver og begrunner strategiene de har brukt. De som har arbeidet baklengs, bør kunne vise, forklare og argumentere for hvordan de fant antall kaker, og hvorfor de brukte motsatte regnearter. Diskusjon og oppsummering må fokusere på strategien i prosessmålet og det faglige målet for timen.

Utfordringen i oppgaven vil i hovedsak være knyttet forståelsen av brøk. Helheten varierer, Nicolai tar en femdel av alle kakene i boksen, mens når Mattias kommer er det `(4)/(5)` som utgjør det hele. Mattias tar en firedel av fire femdeler `(1)/(4) · (4)/(5) = (4)/(20) = (1)/(5)`. Elevene vil erfare at `(1)/(4)` er like mange kaker som `(1)/(5)`, fordi helheten varierer. Noen elever vil også ha problemer med å forstå at de må bruke motsatte regneoperasjoner (legge til antall kaker) når de arbeider baklengs.

Dersom elevene har arbeidet lite med brøkbegrepet, kan det være lurt å arbeide med en lignende oppgave med færre barnebarn.

Småkaker i kakeboksen 

Tre barnebarn var på overnattingsbesøk hos bestefar og bestemor. Der var det en boks med mange kaker. Barnebarna skulle få kaker dagen etter. 

Mattias var eldst og skulle få `(1)/(4)` av alle kakene.

Nicolai var nest eldst og skulle få `(1)/(5)` av alle kakene.

Lille Lisa skulle få to kaker.

Da Lisa hadde lagt seg, kunne ikke Nicolai holde seg lenger.

Han fant kakeboksen og tok `(1)/(5)` av kakene.

Før Mattias skulle legge seg tok han `(1)/(4)` av kakene som da var i boksen.

Lille Lisa var tidlig oppe og tok sine to kaker.

Da bestemor kom, så hun at det bare var 22 kaker igjen.

Hvor mange kaker hadde det vært i boksen?

Matematiske sammenhenger

Prosessmålet for denne aktiviteten er å arbeide baklengs med  problemløsningsstrategier. Elevene blir presentert for et problem, der utgangspunktet er ukjent, så i denne aldersgruppen vil det være naturlig å fremheve strategien å tenke baklengs. De fleste starter med den informasjonen som er kjent, og den står i slutten av teksten.

Elevene må analysere konteksten, reflektere over hva som har skjedd undervegs og hvilken regneart som beskriver hendelsen. De må tolke det barna gjør inn i en matematisk sammenheng. Hver gang småkaker forsvinner fra kakeboksen beskrives det ved hjelp av subtraksjon, og når de skal gå bakover i tid og beskrive den motsatte hendelsen må de bruke addisjon.

Det matematiske målet med aktiviteten er å forstå brøk som del av hel. Elevene må vite at brøkdelene av samme helhet må være like store. De får erfaring med at helheten kan variere, og at to ulike brøker kan utgjøre samme mengde eller antall når helhetene de regnes av forskjellige. Elevene er ofte flinke til å regne brøkdelen av en hel (mengde), men får problemer når de skal gå motsatt vei og finne helheten.

Ved å bruke Gjett og sjekk får elevene kontinuerlig tilbakemelding om løsningen de kommer fram til er riktig (ender de opp med 22 kaker?). Elever som tenker baklengs, bør oppfordres til å kontrollere løsningen sin ved å regne motsatt veg.Noen elever velger strategien Gjett og sjekk. De starter med et mer eller mindre tilfeldig antall småkaker, og prøver seg fram med de opplysningene de får. Strategien fungerer, men kan være tidkrevende på denne type problem.

Refleksjonsspørsmål

• Hvordan vil dere løse oppgaven? Hva vil dere starte med?
• Hvordan vil dere forklare framgangsmåten deres for de andre i klassen?
• Kan dere vise løsningen ved hjelp av andre representasjoner (tegninger/konkreter, tabeller, symboler).
• Hvilken regneart bruker dere og hvorfor? Passer den til konteksten?
• Hvilket regnestykke beskriver situasjonen? Hva forteller regnestykket? Hva har dere funnet ut?
• Fikk de tre barnebarna det antall kaker bestemor hadde planlagt at de skulle få? Begrunn.

Forventede elevresponser 

Svarene avhenger av hvilken strategi elevene velger (se også Observasjonsskjema). Elever som velger strategien Gjett og sjekk, starter med helheten (som de ikke vet).

• Tar utgangspunkt i et mer eller mindre tilfeldig tall. Sjekker om det blir 22 til slutt. Med eller uten plastbrikker.
• Tar utgangspunkt i 5 - gangen, fordi Nicolai skal ha en femdel.
• Tar utgangspunkt i 4 ‧ 5 (fordi det er snakk om firedeler og femdeler).
• Starter med å tegne et tomt rutenett tar deler av det. Tar først en femdel, deretter en firedel av det som er igjen. Ser at 12 av 20 ruter er igjen før Lisa har fått to kaker. Kan ikke være 20 kaker, da ville det vært bare 10 igjen. Utvider brøken slik at det blir 40 kaker totalt (`(12)/(20)` = `(24)/(40)`), da stemmer det med 22 kaker til slutt (24 – 2 = 22).
• Bruker barmodell med utgangspunkt i det som er i boksen: 
  
  

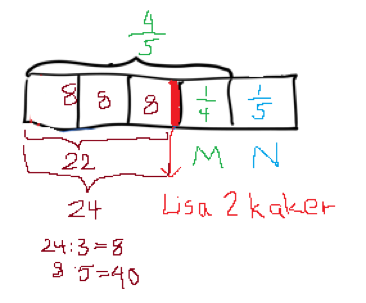
Elever som velger strategien Tenke baklengs, starter med at de vet det er 22 kaker til slutt.

• Legger først til 2 og får 24. Regner videre: (24 : 3) ‧ 4 og får 32. Bygger på med (32 : 4) ‧ 5 og får 40. 
• Noen vil velge samme strategi som over, men bruke plastbrikker eller med støtte i tegning.
• Barmodell med utgangspunkt i det som er igjen til slutt:
  
  

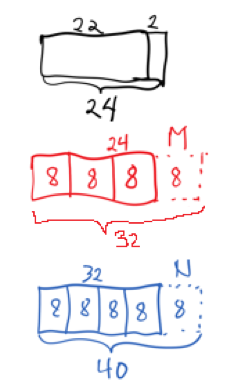
Noen elever vil tenke at helheten er 24 før Lisa har tatt sine kaker og starter med å regne en firedel av det.

• (24 : 4) + 24 → (30 : 5) + 30 → 36
• Som over, men vet bruk av plastbrikker.

Andre tar utgangspunkt i 22. Tar `(1)/(4)` av 22 og får 5,5. Legger til 22 og får 27,5. Tar `(1)/(5)` av 27,5 og får 5,5. Legger til 22,5 og får 28. Noen legger til Lisa sine og får 30.

• Som over, men med plastbrikker. Vil få problemer allerede fra start, med halve brikker.

Kritiske momenter

• Å forstå at en brøkdel avhenger av helheten brøkdelen regnes av, og at helheten kan variere. Noen elever vil regne `(1)/(4)`av 22 eller 24 kaker i stedet for å tenke at de kakene utgjør `(3)/(4)` av helheten før Mattias tok sine kaker. For noen elever vil det være vanskelig å forstå at både `(1)/(5)` og `(1)/(4)` kan utgjøre åtte kaker.
• Å forstå at regnearten blir motsatt når de arbeider baklengs. Antall kaker som ble tatt (subtraksjon), må legges til nå de arbeider baklengs (addisjon). Addisjon og subtraksjon er motsatte regneoperasjoner.

I oppsummeringen bør læreren løfte fram både matematikken som ligger til grunn for løsningen og strategien Tenke baklengs, som inngår i målet for timen.

I matematiske diskusjoner med elever skal læreren prøve å fremme elevenes resonnering og forståelse knyttet til det faglige innholdet som er definert som hensikt for aktiviteten.