Telle i kor med 19 fra 19

Beskrive, bruke og begrunne mønstre og sammenhenger.
Dette opplegget er utviklet som en del av MAM-prosjektet. 

Tavle, gjerne interaktiv tavle, eller flippover.

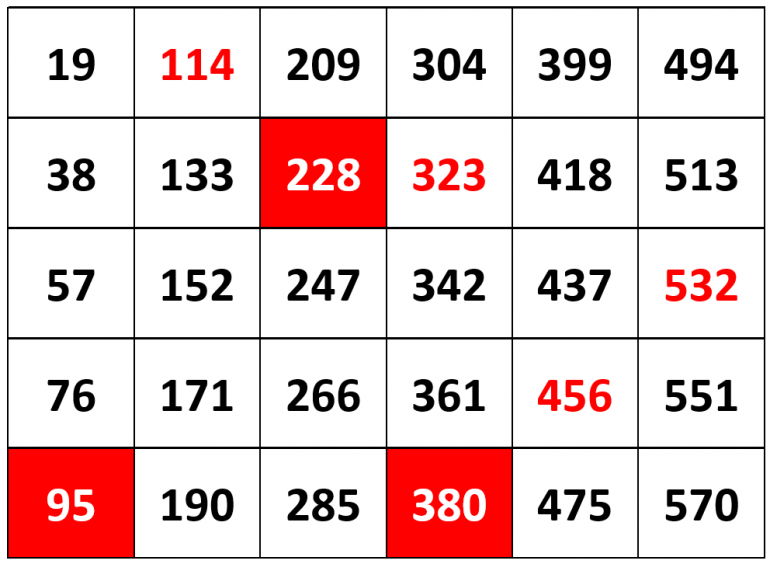
Start tellingen på 19 og tell med 19 om gangen. Skriv tallene i kolonner på fem. Det kan være til hjelp å lage et tomt rutenett på forhånd. Skriv tallet 19 og gi elevene tid til å tenke ut de neste tallene. Elevene sier tallene i kor, samtidig som læreren skriver tallet. Tabellen fylles ut under tellingen, og elevene beskriver hvordan de bruker mønstre og sammenhenger til å finne tallene. Noter elevenes forslag og marker mønstre og sammenhenger i tabellen. Det kan være en idé å spare tabellen med notater slik at den kan brukes igjen senere.

De matematiske sammenhengene i opplegget «telle med 19 fra 19» blir drøftet nærmere nedenfor.

Elevene bør bli oppmerksomme på, og reflektere over hva andre sier. Gi elevene tid til å tenke. Mer om Telle-i-kor-aktiviteter finner du her.

Matematiske sammenhenger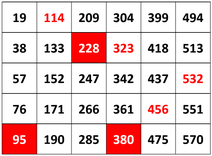 

Tellingen starter på 19 og øker med 19, og vi får egentlig en multiplikasjonstabell for 19. Når vi går nedover i en kolonne øker vi 19 fra rad til rad.
Hopper vi over en rad er økningen 2 · 19 = 38, hopper vi over to rader blir økningen 3 · 19 = 57. For å regne ut 3 · 19, kan én strategi være
å regne 3 · 20 og trekke fra 3 · 1.

Med fem tall i hver kolonne får vi en forskjell på 5 · 19 = 95 mellom naboruter i to kolonner.

I hver rad veksler det mellom to siffer på enerplassen, og på tier-plassen gjentas sifferet to ganger før det minker med én osv. Dette skjer fordi
det adderes 95 fra kolonne til kolonne. 

I hver kolonne øker tierne med to for hver gang, samtidig som enerne minker med én. Det er fordi vi legger til 19, som er to tiere minus en, for hvert steg. Sifferet på hundrerplassen er det samme i hver av de fire første kolonnene. Når vi kommer til 20 · 19, i slutten av fjerde kolonne, har vi plass til en ekstra 19-er til innenfor samme hundrer. Ser vi på tallene i en gitt rad er økningen 95 (20 · 5 – 5), og det innebærer at sifferet på hundrerplassen som oftest øker med én. I hver rad vil det være unntak. I første rad ser vi et unntak allerede etter fjerde tall. 

Vi kan også gå på «skrå», f.eks. fra 342 til 456, ved å addere 114. Vi går da først en kolonne til høyre, adderer 100 (eller 95), og en rad ned, adderer 14 (eller 19), eller i motsatt rekkefølge.

Tabellen er en multiplikasjonstabell for 19. Ved å se på 19 som nesten 20, blir multiplikasjonene mer håndterlige. Vi finner for eksempel 13 · 19 = 247 i tredje rute i tredje kolonne. Hvordan blir dette dersom vi tenker på 19 som (20 – 1)? Klarer elevene å se dette som regnestykket 13 · 19 = 13 · (20 – 1) = 19 = 13 · 20 - 13 · 1. Lede fram mot et generelt utrykk 19 · n = (20 · n) – n.