Andregradsfunksjoner 4

Andregradsfunksjon, funksjonsuttrykk, graf, nullpunkt

PC med GeoGebra

Elevene skal arbeide med andregradsfunksjoner med to nullpunkter. Målet er at de skal oppdage sammenhengen mellom funksjonsuttrykk og nullpunkter.

Aktivitet 1

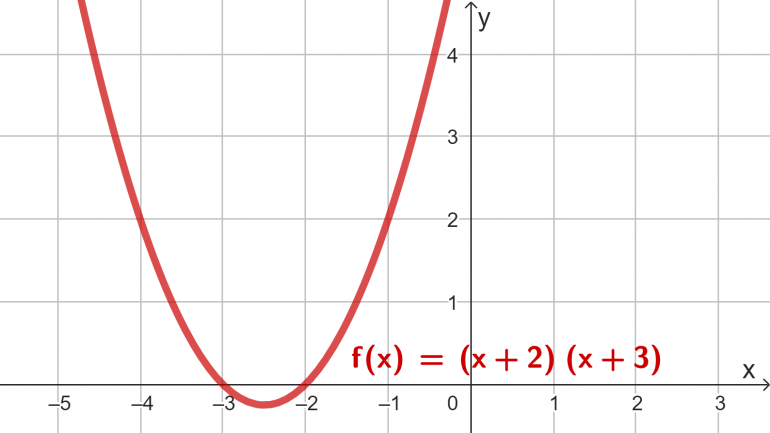
I første aktivitet tegner læreren grafen til f(x) = (x + 2)(x + 3) og leder en klassesamtale med fokus på:

• Hva slags funksjon er f?
• Hva mener vi når vi snakker om nullpunktene til funksjonen?
• Hvor finner vi nullpunktene til funksjonen f, og hva er de?
• Hva er sammenhengen mellom nullpunktene og funksjonsuttrykket?

Kommentar til læreren

Still spørsmålene og la elevene forklare og begrunne. Hvis elevene ikke oppdager det selv i løpet av klassesamtalen, så gjør de oppmerksomme på at hele funksjonsutrykket blir 0 når uttrykket i en av parentesene blir 0. At et produkt blir lik 0 når en faktor er lik 0 er noe mange elever vet, men det er fint for dem å se hvordan de kan utnytte den egenskapen i praksis. Be gjerne elevene å regne ut funksjonsverdien til nullpunktene, f(-2) og f(-3), for å vise det enda tydeligere.

Aktivitet 2

Elevene arbeider med ulike andregradsfunksjoner og nullpunktene deres.

Oppgave 1: Finn nullpunktene til g(x) = (x + 1)(x + 4).

Oppgave 2: Finn nullpunktene til h(x) = (x – 1)(x + 5).

Oppgave 3: Funksjonen i har nullpunkter i x = -2 og x = 3. Lag et funksjonsuttrykk som passer til.

Oppgave 4: Finn nullpunktene til j(x)= x² – 5x + 4.

Kommentarer til læreren

Del oppgavene med elevene og la elevene arbeide i par eller små grupper. Oppfordre dem til å gjette før de sjekker i GeoGebra. Oppgave 1 og 2 er oppgitt på samme form som i aktivitet 1, f(x) = (x + r)(x + s), og elevene kan løse dem på samme måte.

I oppgave 3 er nullpunktene oppgitt, og elevene kan tenke baklengs for å løse oppgaven. I oppgave 4 er funksjonsuttrykket gitt på formen som kanskje er mest kjent for elevene. Elevene kan løse oppgaven ved å finne nullpunktene ved regning eller med GeoGebra. De kan også bruke oppgave 1 som utgangspunkt og endre fortegn.

Oppsummer aktiviteten kort før aktivitet 3. Ha gjerne fokus på sammenhengen mellom oppgave 1 og 4.

Aktivitet 3

Elevene lager lignende oppgaver til hverandre.

Kommentar til læreren

La elevene arbeide i par eller små grupper. Oppfordre dem til å lage varierte oppgaver. Hvis noen trenger hjelp til å komme i gang, kan de bruke uttrykket f(x) = (px + q)(rx + s) som utgangspunkt.

Før de løser oppgavene som medelevene har laget (uten digitale verktøy), skal de gjette hva de tror løsningen kan være. Og etter at de har funnet en løsning, skal de bruke GeoGebra for å kontrollere om løsningen er riktig.

Oppsummering

La elevene oppsummere individuelt ved å lage et notat til fremtidige, glemsomme seg. Notatet bør inneholde eksempler av varierende vanskelighetsgrad og ting eleven mener det er viktig å huske.

Øving

Skriv opp ni oppgaver fordelt på tre ulike vanskelighetskategorier og la elevene velge hvilke oppgaver de gjør selv.

Forslag:

Mild

• Finn nullpunktene til a(x) = (x – 3)(x + 1).
• Finn nullpunktene til b(x) = (5 – x)(x – 2).
• Funksjonen c har nullpunkter i x = 6 og x = -1. Lag et funksjonsuttrykk som passer til.

Medium

• Finn nullpunktene til f(x) = (3x – 1)(x + 2).
• Finn nullpunktene til g(x) = (6 – 3x)(4x + 2).
• Funksjonen h(x) har nullpunkter i x = 1/2 og x = -1. Den har også et toppunkt. Lag et funksjonsuttrykk som passer til.

Spicy

• Finn nullpunktene til n(x)= -x² + 10x – 21.
• Funksjonen m(x) har nullpunkter i x = -3 og x = 2/3. Den har også et toppunkt som har funksjonsverdi større enn 5. Lag et funksjonsuttrykk som passer til.
• Funksjonen o(x) har bare ett nullpunkt. Lag et funksjonsuttrykk som passer til.

Bruk gjerne en blanding av oppgaver som du har forberedt og oppgaver som elevene har laget.