Finn funksjonsuttrykket 1 og 2
Finn funksjonsuttrykket 1 og 2 hører til en serie undervisningsopplegg som er laget i samarbeid med Kikora.
Her finner du oppgaverekkene hos Kikora:
Finn funksjonsuttrykket 1 og Finn funksjonsuttrykket 2
Emne
GeoGebra, Kikora, lineær funksjon, funksjonsuttrykk, x- og y-verdi, stigningstall, konstantledd.
Hensikt
Finne funksjonsuttrykkene til lineære funksjoner ved å ta utgangspunkt i sett med x- og y-verdier. Videre skal elevene bruke kunnskapene de har om funksjonsuttrykk, stigningstall og konstantledd for å finne funksjonsutrykk som tilfredsstiller ulike krav.
Målet er å øke forståelsen av lineære funksjoner, å utvikle effektive strategier for å finne funksjonsuttrykk og å samarbeide med medelev(er) om å utforske matematikk.
Valg av tidspunkt
Du trenger
PC og Kikora.
Aktiviteten
Finn funksjonsuttrykket 1
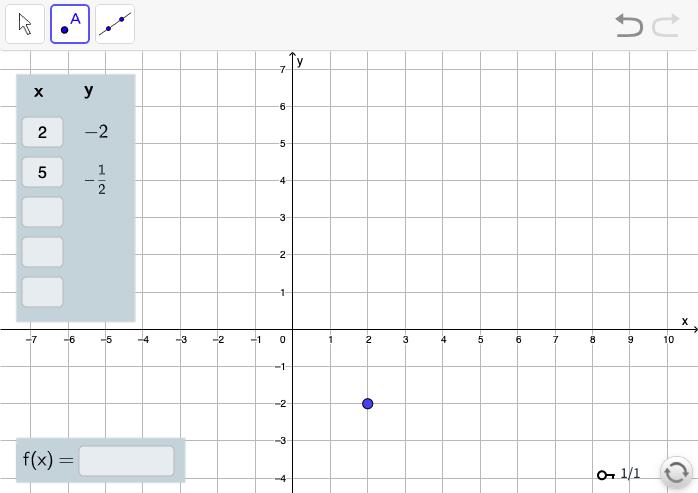
Elevene jobber i par eller i små grupper i Kikora. Programmet lager hemmelige, lineære funksjoner og elevene skal forsøke å finne funksjonsuttrykket som passer til. De skriver inn en x-verdi og Kikora gir dem tilhørende y-verdi. Prosessen gjentas. Elevene kan legge punktene inn i koordinatsystemet og tegne en linje mellom punktene hvis de vil. Når elevene tror at de har funnet riktig funksjonsuttrykk, skriver de det inn i svarfeltet. Kikora tegner da grafen til elevenes funksjonsuttrykk i koordinatsystemet og forteller om det er riktig.
Etter at alle elevene har løst noen oppgaver, skal de reflektere individuelt over følgende spørsmål:
-
Hvor mange x-verdier må dere ha for å finne funksjonsuttrykket til en lineær funksjon?
-
Hvilke x-verdier er «lure» å spørre Kikora om og hvorfor?
-
Hvordan kan dere finne funksjonsuttrykket raskest og enklest?
Deretter oppsummerer klassen aktiviteten og refleksjonsspørsmålene. Læreren løfter fram effektive strategier for å finne funksjonsuttrykkene.
Kommentarer til læreren
Funksjonene i oppgaverekken er tilfeldige. Det betyr at elevene kan jobbe seg gjennom hele opplegget flere ganger med nye funksjonsuttrykk. I tillegg medfører det at elevgruppene ikke nødvendigvis har de samme oppgavene. Vanskelighetsgraden øker utover i oppgaverekken. Hvis elevene trykker på Oppdater i Grafikkfeltet, får de en ny funksjon med samme vanskelighetsgrad. På denne måten kan elevene arbeide over lengre tid på samme nivå. Ved å la elevene jobbe sammen på én PC må de samarbeide og diskutere.
Finn funksjonsuttrykket 2
Elevene arbeider i par eller i små grupper i Kikora. Opplegget består av to oppgaverekker og en oppsummeringsoppgave. Første rekke består av oppgaver hvor elevene skal finne funksjonsuttrykket til en funksjon som går gjennom to gitte punkter, med svaralternativer. Andre rekke inneholder oppgaver hvor de skal finne en funksjon som tilfredsstiller ulike krav. Siste oppgave består av et sett med avkryssingsoppgaver som oppsummerer temaet.
Til slutt oppsummerer klassen aktiviteten ved at elevene presenterer hvordan de tenkte for å løse utvalgte oppgaver.
Kommentarer til læreren
Det er viktig at elevene vet hva det betyr at grafen til en funksjon går oppover eller nedover før de starter med oppgavene. Det er ikke alle elever som vet at retningen til en lineær graf er bestemt av hva som skjer når x øker (oppover hvis y øker når x øker og nedover hvis y minker når x øker).
Elevene kan zoome inn og ut og flytte på Grafikkfeltet dersom de ikke er fornøyde med utsnittet som er gitt. I noen av oppgavene skal elevene skrive inn funksjonsuttrykket i en tekstboks. Dersom de skriver feil uttrykk og ønsker å endre deler av det, trykker de i tekstboksen og bruker piltastene for å flytte markøren.
Det finnes mange måter å løse disse oppgavene på. Når elevene arbeider sammen, må de forklare hva de tenker og argumentere for hvorfor de mener noe. Sammen kommer de fram til gode, varierte strategier. Læreren bør se og høre på elevenes arbeid og samtaler underveis, og gjerne notere slik at hun har et godt grunnlag for å velge ut oppgavene til oppsummeringen. Det er ikke nødvendig at alle elever har løst alle oppgavene før oppsummeringen starter.
I oppgavene i første oppgaverekke har elevene mulighet til å vise linjen dersom de ikke klarer å se for seg hvordan linjen ser ut, når de bare ser punktene. Læreren bør utfordre elevene til å prøve uten å vise linjen først slik at de får trening i å visualisere lineære funksjoner. Oppgavene hvor elevene skal finne funksjoner som står normalt på en gitt funksjon, er beregnet på elever som blir raskt ferdige og/eller trenger ekstra utfordringer.
Rammeplanmål/Kompetansemål
- Grunnskole
- Kompetansemål etter 10. trinn
- utforske og samanlikne eigenskapar ved ulike funksjonar ved å bruke digitale verktøy
- rekne ut stigingstalet til ein lineær funksjon og bruke det til å forklare omgrepa endring per eining og gjennomsnittsfart
- Videregående
- Vg1P
- bruke digitale verktøy i utforsking og problemløysing knytt til eigenskapar ved funksjonar, og diskutere løysingane
- identifisere variable storleikar i ulike situasjonar og bruke dei til utforsking og generalisering
- tolke og bruke funksjonar i matematisk modellering og problemløysing
- Vg1T
- formulere og løyse problem ved hjelp av algoritmisk tenking, ulike problemløysingsstrategiar, digitale verktøy og programmering
- identifisere variable storleikar i ulike situasjonar, setje opp formlar og utforske desse ved hjelp av digitale verktøy
- Vg2P
- utforske strategiar for å løyse likningar, likningssystem og ulikskapar og argumentere for tenkjemåtane sine
