Introduksjon til derivasjon

Funksjoner, polynom, derivasjon, momentan vekstfart

PC med GeoGebra og elevark.

I dette opplegget skal elevene undersøke den momentane vekstfarten til polynomfunksjoner og etter hvert bli kjent med begrepet derivasjon. Begrepene momentan vekstfart i punktet og stigningstallet til tangenten i punktet er sentrale. Bruk begrepene hyppig i samtale med elevene. Målet er at de til slutt vet at derivasjon faktisk er å finne momentan vekstfart til en funksjon i et punkt, at vekstfarten representeres ved stigningstallet til tangenten i punktet, og at det er denne vekstfarten vi kaller den deriverte til funksjonen i punktet. De skal ikke bare assosiere derivasjon med derivasjonsreglene de etter hvert lærer. Merk at vi ikke innfører selve ordet derivasjon før elevene har arbeidet med opplegget en god stund.

Elevene skal oppdage mønstrene selv. Nesten alle tabellene har tomme rader hvor elevene kan velge egne x-verdier eller funksjoner. Når elevene tror de har funnet et mønster, kan de selv teste om det stemmer for andre tilfeller. Hvis mønsteret elevene har funnet er feil, kan samme metode avsløre at noe ikke stemmer, og at de må studere problemet på nytt. Utfordre elevene til å prøve seg frem.

Mens de arbeider, har læreren mulighet til å gå rundt og observere og snakke med dem. Prøv å oppmuntre elevene, og sett dem på sporet uten å gi dem løsningene. Det er fornuftig å ta noen stopp underveis der klassen snakker sammen om det de arbeider med, og det de har kommet frem til. Hvis læreren ønsker at noen elever skal presentere egne løsninger for klassen, er det lurt å avtale dette på forhånd.

Aktivitet 1

Elevene starter med aktivitet 1 på elevarket. De skal tegne polynomfunksjoner i GeoGebra og undersøke stigningstallet til tangenten i gitte punkter. Målet er at de skal finne et mønster for stigningstallet til tangentene.

For alle funksjonene gjelder følgende:                                     

• Lag en ny fil i GeoGebra til hver funksjon.
• Lag et punkt på grafen og tegn tangenten til grafen i punktet. Tips: Verktøyet Stigning viser stigningstallet til tangenten. 
• Dra i punktet for å finne stigningstallet til tangenten i gitte punkter. Noter i skjemaet.
• Kan du gjette hva stigningstallet til tangenten vil bli i et annet punkt på grafen? Skriv det du gjetter i skjemaet og kontroller etterpå i GeoGebra.

Kommentarer til læreren

La elevene arbeide i eget tempo og oppsummer i helklasse etterpå. Hvilke mønster har elevene funnet? Hvordan har de beskrevet mønstrene? Har de brukt ord, symboler eller kanskje en tegning? Skriv opp forslagene på tavla. Diskuter likheter og ulikheter. For eksempel er «Jeg dobler x’en» eller «2x» to representasjoner av samme uttrykk. I begynnelsen bruker elevene ofte begge representasjonene, men etter hvert vil nok de fleste synes det enklest å beskrive mønsteret med et algebraisk uttrykk.

Aktivitet 2

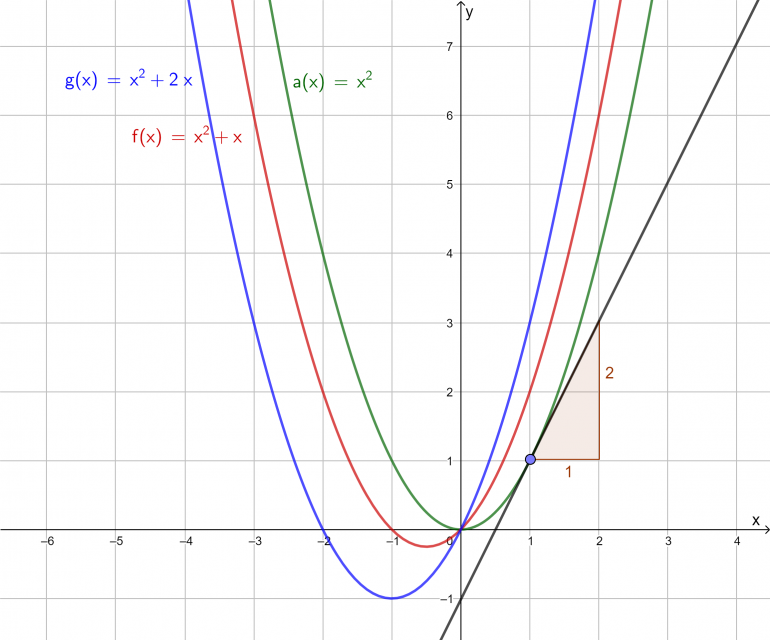
I denne aktiviteten skal elevene sammenligne utvalgte funksjoner. Målet er at de skal finne ut hvordan små endringer i funksjonsuttrykket påvirker stigningstallet til tangenten.

Kommentarer til læreren

Elevene tegner tre og tre funksjoner i samme GeoGebra-fil. Bruk god tid til å sammenligne uttrykkene, grafene og stigningstallene. Hva er likt, og hva er forskjellig? Hva er mønsteret? Hvordan kan elevene uttrykke det, både med ord og algebraisk? Finnes det flere funksjoner som følger samme mønster?

Andre spørsmål:

• Hvorfor får tangentene til `a(x)=x^(2)` og `c(x)=x^(2) + 3` samme stigingstall i samme x-verdi?
• Hvorfor må stigningstallet til tangentene til `a(x)=x^(2), j(x)=x^(3)` og `k(x) = x^(4)` være forskjellig ved samme x-verdi?
• Hva må regelen være når vi har funksjoner med flere ledd?

Aktivitet 3

Aktiviteten starter med en helklassesamtale hvor læreren introduserer begrepet derivasjon og skrivemåten med den lille «apostrofen». Når vi deriverer en funksjon, får vi en ny funksjon som gir oss momentan vekstfart (tangentens stigningstall) i et hvilket som helst punkt på grafen. Til slutt skal elevene generalisere reglene for derivasjon.

Kommentarer til læreren

Elevene skal først skrive ned mønstrene fra aktivitet 1 og 2. Utfordre dem til å bruke algebraiske uttrykk. Så skal elevene prøve å finne en generell regel for derivasjon av polynomer ved å undersøke polynomer av høyere grad enn i de to første aktivitetene. For mange elever er det motiverende å finne mønsteret på egen hånd. La de gjerne teste funksjoner de velger selv også.

Etter at regelen `q(x)=x^n` gir `q'(x)=nx^(n-1)` er etablert, er det nyttig å se spesielt på tilfellene der eksponenten er 1 og 0. Til slutt skal elevene forklare hva derivasjon er med ord. En mulig elevforklaring kan være at derivasjon gir oss den momentane vekstfarten (tangentens stigningstall) i et hvilket som helst punkt på grafen. Eller de kan skrive at den deriverte til et polynom vil være en grad lavere. Det forklarer hvorfor to funksjoner har den samme deriverte hvis bare konstantleddet er forskjellig.

Oppsummering

Elevene har fått varierte erfaringer med vekstfart og derivasjon. Bruk elevenes beskrivelse av derivasjon som utgangspunkt for å snakke om hva derivasjon er. De har også funnet en generell regel som gjør at de kan derivere alle polynomfunksjoner. I oppsummeringen er det viktig å vektlegge sammenhengen mellom momentan vekstfart til en funksjon i et punkt, stigningstallet til tangenten i punktet og den deriverte i punktet. Test elevenes forståelse ved å be de finne den momentane vekstfarten til forskjellige funksjoner ved en gitt x-verdi.

Oppfordre elevene til å bruke metoden fra dette opplegget når de senere skal derivere ulike funksjoner. Da kan de sjekke at reglene stemmer. Uttrykkene for den deriverte gir elevene mulighet til å regne ut den momentane vekstfarten til en funksjon i et hvilket som helst punkt.