Mønster i tidlig tallforståelse
Vi møter mønster i mange områder i livet rundt oss, i både ukedager, skoledager, danserytmer, spill, bøker og når vi lager mønster med for eksempel perler og klosser.
Mønster i faget matematikk er regelmessigheter og strukturer i tall og figurer. Så og si all matematikk er basert på mønster (Mulligan & Mitchelmore, 2009). Uansett om elevene arbeider med tall eller figurer, må fokuset være på å oppdage og beskrive mønsteret, å fortsette mønsteret og på å kopiere et mønster som for eksempel en annen elev har laget.
Elever i skolen vil i all hovedsak møte mønster i tre sammenhenger/kontekster (Gould et al., 2023).
- Repeterende mønster
- Romlige ordnede mønster
- Voksende mønster
Repeterende mønster
Repeterende mønster er mønster som har en gjenkjennbar repeterende syklus av elementer. Elementene kan for eksempel være tall, bokstaver, figurer eller farger.
Eksempel:
 |
Repeterende elementer: grønn-oransje |
 |
Repeterende elementer: maur-eple-tre |
 |
Repeterende elementer: ABc |
 |
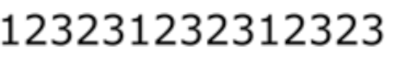Repeterende elementer: 12323 |
For elever handler det om å se at det er et mønster og kunne uttrykke hva dette mønsteret består av. Ved å endre på egenskapene til ett eller flere elementer i et mønster som størrelse, farge, orientering og antallet av elementer som repeteres, kan det repeterende mønsteret gjøres mer komplekst (Zazkis & Liljedahl, 2002).
Romlige ordnede mønster
Romlige ordnede mønster handler om mønster i mengder, geometriske figurer og i organisering av data (Gould et al., 2023).
Mønster i mengder
Å se etter mønster i mengder handler om å oppdage hvordan elementene er plassert for lettere å kunne finne antallet i mengden. For eksempel vil mengden ⚄ kunne gjenkjennes som 5 uten å telle hver enkelt prikk. Dette kalles subitizing. Subitizing innebærer at vi med et blikk kan gjenkjenne antall objekter i en mengde og koble tallordet til mengden.
Når vi umiddelbart gjenkjenner hvor mange objekter det er i en mengde, kaller vi det perseptuell subitizing. Men om vi umiddelbart gjenkjenner hvor mange objekter det er i delmengder og setter delmengdene sammen til hele mengden kalles det konseptuell subitizing (Clements & Sarama, 2020). For eksempel setter vi umiddelbart sammen to terninger med fem øyne på hver (to femmere), til en mengde på ti øyne (en tier).
⚄ ⚄ 🡲 10
For å finne antall elementer i en større mengde, kan man se etter mønstre i hele mengden. Groupitizing handler om å kunne dele opp en større mengde til håndterbare mindre mengder for kjapt og enkelt kunne finne antall elementer i mengden, uten å telle hvert enkelt element (Starkey & McCandliss, 2014).
I en mengde med åtte elementer, som vist nedenfor, er det mulig å se mønsteret på ulike måter. Eksempelet viser to mulige måter å se mønsteret på.
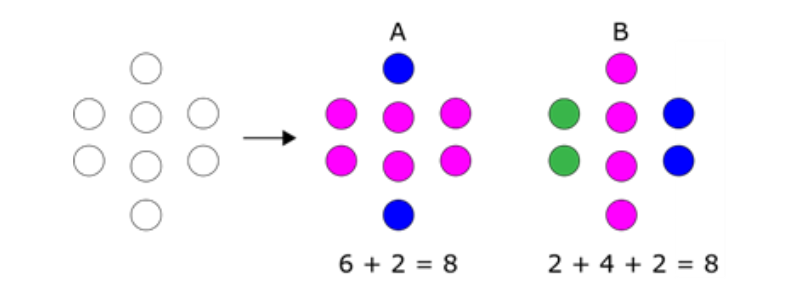
Mønster i geometriske figurer
Telling av større mengder kan skape et behov for å strukturere både de elementene som er telt og de som ikke er telt, noe som vil gjøre tellingen mer oversiktlig. Det å kunne se for seg hvordan elementer er organisert er en grunnleggende mental prosess som ligger til grunn for elevers tallfesting av mønster i geometriske figurer (Mulligan & Mitchelmore, 2013).
Mønster i geometriske figurer kan relateres til subitizing og groupitizing, ved at man bruker mentale bilder for å se et mønster i hvordan en figur er bygd opp, for eksempel antall ruter en figur består av.
Barn er i utvikling når de strukturerer mønster i geometriske figurer. Tabellen nedenfor viser beskrivelser for de ulike utviklingsnivåene og typiske eleveksempler, hvor barn har fått i oppgave å tegne et 2 x 3 rutenett som de kun har sett i noen få sekunder. Deretter har de tegnet rektangelet ut fra hukommelsen (Mulligan & Mitchelmore, 2013).
| Struktureringsnivå | Beskrivelse | Eksempel |
|---|---|---|
| Prestructural (Før-strukturering) |
Spredte ruter eller ei rekke med ruter. |  |
| Emergent (Begynnende) |
Forsøk på å tegne et rutenett, men verken antall ruter eller strukturering av rutene er riktig presentert. |  |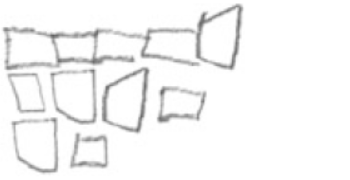
| Partial structural (Delvis strukturering) |
Et ufullstendig rutenett eller et rutenett som ikke er korrekt i form av antall ruter. For eksempel:
|
  
|
| Structural (Strukturert) |
Et rutenett med riktig antall ruter der rutene henger sammen, men hver rute er tegnet separat. |  |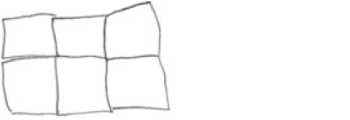
| Advanced (Avansert) |
Et rutenett med riktig antall ruter som er tegnet med sammenhengende horisontale og vertikale linjer. |  |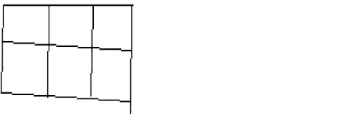
Legg merke til at begge de to siste nivåene gir et riktig bilde av rutenettet, men det siste nivået viser en mer avansert forståelse som muliggjør generalisering til lignende oppgaver.
Organisering av data
I begynneropplæringen lager man ofte søylediagram der søylene viser elementet som telles. Etter en tur i skogen kan et diagram se slik ut:
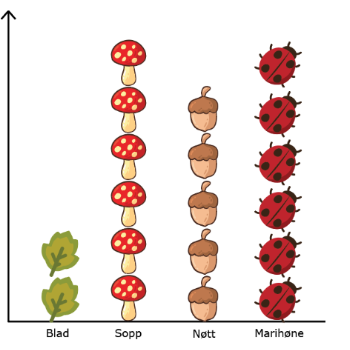
Her er data organisert etter type og de ulike elementene er stablet oppå hverandre. Begge i et bestemt mønster. Organisering av data bidrar til at antallet, kardinaltallet, i de ulike mengdene synliggjøres systematisk. Ved å se på mønstret i diagrammet kan en enkelt se sammenhenger mellom mengdene og estimere hvor det er like mange, flest, færrest osv. Dette forutsetter at hvert element i diagrammet har samme høyde.
Voksende mønster
Voksende mønster handler om tallfølger eller figurer som øker eller avtar i antall eller størrelse.
Eksempel med samme tallfølge:
Hvor det ukjente tallet er plassert, avgjør vanskegraden. Det er enklest å finne det neste tallet og mest krevende å finne tallet i starten til en tallfølge.
Finne det neste tallet:
3 4 5 6 _
Finne det manglende tallet:
3 4 _ 6 7
Finne tallene i starten til en tallfølge:
_ 4 5 6 7
Eksempel med figurer:
Mønster med figurer handler om alt fra enkle mønster som øker med én i antall:
Til mer komplekse figurer der det voksende mønsteret kan sees på mange ulike måter:
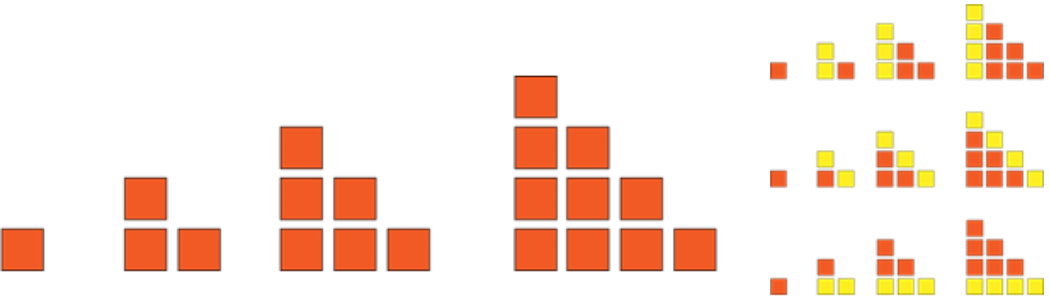
De gule rutene viser ulike måter å se hvordan dette mønsteret vokser.
I slike aktiviteter, spesielt med figurmønster, må det fokuseres på å beskrive hva som forblir det samme og hva som endres fra en figur til den neste. Dette danner grunnlaget for arbeid med mønster, variabler og generalisering.
Referanser
Clements, D. H., & Sarama, J. (2020). Learning and teaching early math: The learning trajectories approach. Routledge.
Gould, T., Watson, F., & Rycroft-Smith, L. (2023). Developing concepts of pattern. Cambridge Mathematics. Retrieved 20.06 from https://www.cambridgemaths.org/for-teachers-and-practitioners/espresso/view/developing_concepts_of_pattern/
Mulligan, J., & Mitchelmore, M. (2009). Awareness of pattern and structure in early mathematical development. Mathematics Education Research Journal, 21(2), 33–49.
Mulligan, J. T., & Mitchelmore, M. C. (2013). Early awareness of mathematical pattern and structure. In L. D. English & J. T. Mulligan (Eds.), Reconceptualizing early mathematics learning (pp. 29–45). Springer.
Starkey, G. S., & McCandliss, B. D. (2014). The emergence of “groupitizing” in children’s numerical cognition. Journal of Experimental Child Psychology, 126, 120–137.
Zazkis, R., & Liljedahl, P. (2002). Generalization of patterns: The tension between algebraic thinking and algebraic notation. Educational Studies in Mathematics, 49, 379–402.