Skredder og skjerf

Emne
Divisjon med brøk. Problemløsing. Resonnering.
Hensikt
Se på ulike løsningsstrategier i divisjon og sammenhengen mellom disse. Spesielt fokus på hva som skjer med svaret når divisor minker/øker med en gitt faktor. Elevene får utforske divisjon med brøk ved hjelp av ulike representasjoner – tegninger/konkreter, tallinje, symboler.
Bruk av Samtaletrekk kan være til hjelp i å lede den matematiske diskusjonen i klassen.
Valg av tidspunkt
Du trenger
Aktiviteten
Presenter oppgaven muntlig for elevene. Elevene skal finne ut hvor mange skjerf skredderen kan sy av seks meter stoff, når han trenger en halv meter stoff til hvert skjerf. Elever arbeider to og to og kommer med forslag, som også skal utrykkes skriftlig. I en felles diskusjon noterer læreren forslagene på tavla. Fokuser på regneoperasjon og hvilket regnestykker som gir svar på problemstillingene. Utfordre elevene til å argumentere for sine svar.
Presenter også de to neste oppgavene muntlig for elevene. Skredderen skal sy andre typer skjerf, først noen som er kortere enn det første, deretter noen som er lengre enn de første. Elevene skal finne antall skjerf, og om det blir færre eller flere enn i første oppgave. Utfordre elevene på om de kan finne løsninger uten å starte helt på nytt igjen, og begrunne disse. Elevene arbeider fortsatt to og to og utarbeider forslag på store ark/plakater slik at de andre elevene i klassen får del i hvordan de har tenkt. Elevene forklarer og begrunner. Oppfordre elevene til å bruke ulike representasjoner.
Læreren observerer arbeidet og velger rekkefølgen på presentasjonene (velger om lærer skal oppsummere eller om elevene skal presentere). Diskusjon og oppsummering må fokusere på det faglige målet for timen.
Skredder og skjerf
En skredder har seks meter stoff og skal sy skjerf.
a) Til hvert skjerf trenger han `(1)/(2)`meter stoff. Hvor mange skjerf kan han sy?
b) Skredderen skal sy en annen type skjerf som er slik at det trengs `(1)/(4)` meter stoff for hvert skjerf? Blir det flere eller færre skjerf enn i sted? Kan du finne ut hvor mange skjerf det blir uten å regne på nytt? Forklar og begrunn.
c) For en tredje type skjerf trengs det `(3)/(4)`meter stoff til hvert skjerf. Blir det flere eller færre skjerf enn i b), enn i a)? Kan man finne ut hvor mange skjerf det blir uten å regne (helt) på nytt? Forklar og begrunn.
Ekstra:
- Hva med regnestykket 10 : `(5)/(4)` ? Hvor mye blir det og hvordan vet du det? Hva slags situasjon/regnefortelling kunne passer til det regnestykket? (Hvis elevene ikke svarer kan lærer tipse om skredder og skjerf.
Matematiske sammenhenger
I denne aktiviteten får elevene erfaring med målingsdivisjon. Spørsmålet er knyttet til antall skjerf skredderen kan sy. Det er ikke opplagt for elevene at de ut fra denne konteksten skal bruke divisjon. Mange elever knytter divisjon til en mengde de deler likt, med etterfølgende spørsmål: Hvor mye blir det på hver? (delingsdivisjon).
I denne oppgaven er spørsmålet: Hvor mange skjerf kan skredderen sy? Mange elever vil tenke at skredderen får to skjerf på en meter. De finner løsningen, 12 skjerf, ved å multiplisere seks med to. Utfordre elevene til å reflektere rundt regnearten de velger og hva regnestykket forteller (Hva er det sekstallet representerer? Hva med totallet? Hvor er tallet `(1)/(2)`?)
Se på ulike løsningsstrategier i divisjon og sammenheng mellom disse. Ha spesielt fokus på hva som skjer med svaret når divisor minsker/øker med en gitt faktor. For eksempel at `(1)/(4)` er halvparten av `(1)/(2)` og at tallet `(3)/(4)` er tre ganger større enn `(1)/(4)`.
Diskuter motsatte regneoperasjoner og inverse tall (Hvorfor er det å dividere med en halv det samme som å multiplisere med to? Hvorfor fungerer huskeregelen mange lærer seg i divisjon med brøk: Snu den bakerste brøken og multipliser).
Refleksjonsspørsmål
- Hvordan vil dere løse oppgaven? Hva vil skredderen gjøre med tøystykket på seks meter?
- Hvordan vil dere forklare framgangsmåten deres for de andre i klassen?
- Kan dere vise løsningen ved hjelp av andre representasjoner (tegninger/konkreter, tallinje, symboler).
- Hvilken regneart passer til konteksten?
- Hvilket regnestykke beskriver situasjonen? Hva forteller regnestykket? Hva har dere funnet ut?
- Hva hvis skredderen brukte tre meter per skjerf? Hvilket regnestykket ville passe til konteksten? (tre går to ganger opp i seks)
- Hva hvis han brukte en meter per skjerf? Regnestykke? (en går seks ganger opp i seks)
- Hva ble regnestykket da han trengte `(1)/(2)` meter per skjerf? Forklar og begrunn. (`(1)/(2)` går 12 ganger opp i seks)
Forventet elevrespons
Trenger `(1)/(2)` meter per skjerf
- Lager en tegning av seks meter stoff, deler alle i to og får tolv biter.
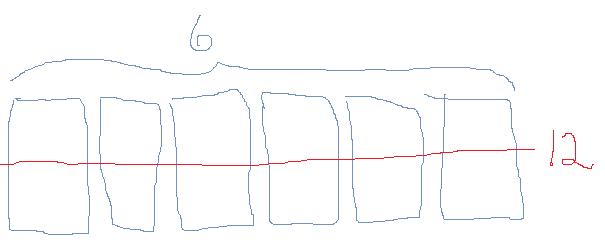
- Skriver: 2s = 1m, 4s = 2m, 6s = 3m,... 12s=6m.
Benevningen meter kan forkortes til m, men vær oppmerksom når elevene bruker s for antall skjerf. Som variabel betyr s lengden på skjerfene, ikke antall skjerf.
Trenger `(1)/(4)` meter per skjerf
- siden en firedel er halvparten av en halv, så da dobler vi bare 12 siden det var svaret på den forrige oppgave, og da blir det 24.
- De blir mindre og da blir det flere. Siden det er halvparten, så blir det dobbelt så mange.
- Fire skjerf, gir 4 i en meter. Og så tar vi 4 skjerf gange 6 som er 24
- Prøver med tallinjer eller tabell (se sammenhenger)
 |
 |
Kritiske momenter
Konteksten handler om lik fordeling, altså divisjon. Med utgangspunkt i konkrete situasjoner oppdager vi at det er to typer problemer som svarer til divisjon, delingsdivisjon og målingsdivisjon. Delingsdivisjon er deling i mindre mengder, der vi skal finne hvor mye det er i hver mengde. Hvis tre barn skal dele seks sjokolader mellom seg, får de to hver. I målingsdivisjon derimot skal man finne antall delmengder, ikke størrelsen av hver enkelt. Vi har seks sjokolader, og hvert barn skal få to sjokolader. Hvor mange barn er det nok til? Ofte arbeides det i skolen mer med kontekster innen delingsdivisjon, og da kan det være utfordrende for elever å kjenne igjen en kontekst med målingsdivisjon.
Kontekster med delingsdivisjon fungerer ofte dårlig med desimaltall eller brøk, men målingsdivisjon vil fortsatt fungere: Sjokoladene kan ikke deles på halve barn, men hvert barn kan godt få en halv sjokolade. Derfor er det viktig at elevene møter både delingsdivisjon og målingsdivisjon allerede mens de jobber med divisjon av heltall.
Eksempel på delings- og målingsdivisjon i oppgaven Skredder og skjerf:
Skredderen skal sy skjerf av seks meter tøy.
Delingsdivisjon: Skredderen skal lage tre like lange skjerf. Hvor langt blir hvert skjerf? Svaret er to meter.
Målingsdivisjon: Skredderen skal lage skjerf som er tre meter lange. Hvor mange skjerf? Svaret er også her to, men nå er det snakk om to skjerf.
I matematiske diskusjoner med elevene skal læreren prøve å fremme elevenes resonnering og forståelse knyttet til det faglige innholdet som er definert som hensikt for aktiviteten.
Rammeplanmål/Kompetansemål
- Grunnskole
- Kompetansemål etter 5. trinn
- utvikle og bruke ulike strategiar for rekning med positive tal og brøk og forklare tenkjemåtane sine
- formulere og løyse problem frå eigen kvardag som har med brøk å gjere
- beskrive brøk som del av ein heil, som del av ei mengd og som tal på tallinja og vurdere og namngi storleikane
- Kompetansemål etter 6. trinn
- formulere og løyse problem frå sin eigen kvardag som har med desimaltal, brøk og prosent å gjere, og forklare eigne tenkjemåtar
- Kompetansemål etter 7. trinn
- utvikle og bruke formålstenlege strategiar i rekning med brøk, desimaltal og prosent og forklare tenkjemåtane sine
- Kompetansemål etter 8. trinn
- utvikle og kommunisere strategiar for hovudrekning i utrekningar
