Speiling om linjer og sidekanter
Speiling om linjer og sidekanter hører til en serie undervisningsopplegg som er laget i samarbeid med Kikora.
Her finner du oppgaverekkene hos Kikora: Speiling om linjer og sidekanter.
Emne
GeoGebra, Kikora, speiling, trekanter, firkanter.
Hensikt
Få en dypere forståelse for begrepet speiling.
Valg av tidspunkt
Du trenger
Blanke ark, PC med GeoGebra og Kikora (må ha tilgang til internett).
Aktiviteten
Aktivitet 1
Aktiviteten er ment som en introduksjon eller repetisjon av speiling. Elevene skal brette ark og speile figurer. Bretten skal være speilingslinjen.
Læreren gir oppgavene muntlig eller skriver de opp på tavla.
- Brett et A5-ark tilfeldig. Bretten skal være speilingslinjen. Pass på at bretten ikke er parallell med sidekanten til arket.
- Tegn en mangekant på den ene siden av bretten slik at ett hjørne ligger på bretten.
- Tegn speilbildet av figuren på den andre siden av bretten.
- Brett et nytt A5-ark slik at bretten blir en skrå speilingslinje.
- Tegn en mangekant der ingen punkter berører speilingslinjen. Speil mangekanten om bretten.
Kommentarer til læreren
Elevene kan løse oppgaven på mange måter:
- Brettet ark på mykt underlag og tegne over figuren slik at det blir et avtrykk.
- Brettet ark og markere hjørner med blyant eller en passerspiss.
- Brettet ark mot et vindu.
- Åpent ark og tegne på måfå.
- Åpent ark og bruke linjal, sånt omtrentlig.
- Åpent ark og konstruere speilbildet med normale linjer.
- Åpent ark og konstruere speilbildet med hjelp av sirkler.
Vær oppmerksom på om noen elever tegner speilbildet som om speilingslinjen er parallell med sidekanten. Det er en vanlig misoppfatning som er viktig å være bevisst på. Læreren må legge til rette for at elevene som er i en slik misoppfatning kan utvikle en bedre begrepsforståelse om speiling. Oppgavene i dette undervisningsopplegget vil utfordre tankegangen til elevene og skape et behov for å endre tankemønster.
Noter hvilke strategier elevene bruker og tenk over hvilken rekkefølge elevene skal presentere løsningene sine i. Legg spesielt merke til feilløsninger siden de kan være nyttige for å diskutere egenskapene til speiling. Elevene skal komme frem til at linjene mellom punkt og speilingspunkt står normal på speilingslinjen og at avstanden fra speilingslinjen til punkt og speilingspunkt er like stor.
Aktivitet 2
I denne aktiviteten begynner elevene med oppgaverekkene på Kikora sin plattform. De sitter sammen i par med én PC. Arbeidet i Kikora blir avbrutt av korte helklassesamtaler.
Læreren instruerer muntlig:
- Åpne Kikora og velg Speiling om linjer om sidekanter.
- Bruk god tid og gjør gjerne en oppgave flere ganger.
- Trykk på snurrehjulet for å starte på nytt.
- Husk å velge Flytt før dere endrer farge eller drar i figurer.
I første oppgaverekke (to oppgaver) lager elevene tegninger ved at de drar i punkter. Bruk god tid og be elevene ha fokus på hva som skjer når de beveger på et punkt. Kikora gir elevene godkjent (et steg blir grønt) når de har beveget et stykke på punktene.
I andre oppgaverekke (tre oppgaver) blir elevene kjent med verktøyet Speil objekt om linje og det skal de bruke i resten av oppgavene. I disse oppgavene bruker elevene sidekantene som speilingslinjer. Elever som trenger flere utfordringer, kan for eksempel lage fargerike mønstre av figurene eller speile rombene slik at de ser ut som terninger. Det er ikke nødvendig at alle elevene blir ferdige med alle oppgavene i oppgaverekken.
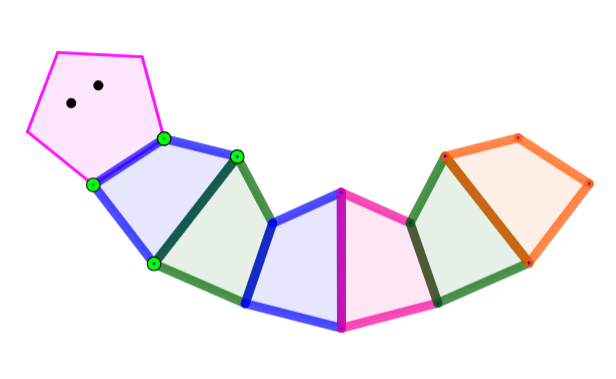
I oppgave 3 skal elevene lage en larve ved å speile firkanter. Like viktig som et pent sluttresultat, er at elevene leker med oppgaven. De må få anledning til å oppdage fordelen ved å arbeide i GeoGebra. Hvorfor beveger hele larven seg hvis elevene drar i ett punkt? Hva må de gjøre for at larven skal bli liten eller kanskje veldig stor?
Etter at alle elevene har arbeidet en stund med oppgave 3, samler læreren klassen til en kort felles oppsummering. Ha fokus på hvordan larven beveger seg og hva som gjør at den blir liten eller stor.
I fjerde oppgaverekke skal elevene speile en figur flere ganger inntil den dekker en annen figur. Det finnes mange veier til mål så elevene kan gjerne gjøre oppgavene flere ganger. Trykk på snurrehjulet for å starte på nytt.
Avslutt aktiviteten med en klassesamtale om erfaringene elevene har fått. Sørg for at begrepene speiling, speilbilde, speilingslinje og symmetrilinje blir nevnt.
Kommentarer til læreren
Det er en fordel at elevene er litt kjent med GeoGebra før de starter med oppgavene. De bør vite når de må trykke på Flytt, hvordan de beveger på objekter, hvordan de bruker verktøy og hvordan de endrer farger. Dette kan de lære i Lær GeoGebra: Geometri.
Hver av disse oppgaverekke består av liknende oppgaver. Elevene får derfor erfaringer de kan dele i helklassesamtale så lenge de har gjort en oppgave i hver oppgaverekke. Det er derfor ikke nødvendig at elevene gjør alle oppgavene. Læreren kan be elever som blir raskt ferdig om å gjøre oppgavene flere ganger med ulikt resultat. På den måten vil alle elever ha mulighet til å bruke den tiden de trenger.
Aktivitet 3
Elevene arbeider videre på Kikora. Oppgave 5 er en flervalgsoppgave. Det er viktig at elevene beveger figuren før de svarer på spørsmålene. Vi anbefaler at læreren viser bildet på storskjerm for en felles gjennomgang av spørsmålene. Pass på å bevege alle punktene i originalfiguren, samt å undersøke hva som skjer om dere drar et punkt til eller over speilingslinjen.
De siste to oppgaver henger sammen. Oppgaven 6.1 er en forberedelse til den siste oppgaven. Her skal elevene speile en figur om forskjellige speilingslinjer. Til slutt skal de teste om oppgaven er løst riktig ved å dra i hjørnene til trekanten.
I den siste oppgaven skal elevene speile en trekant, en firkant og en femkant, tre ganger til det er tre figurer i de fire områdene. Målet med oppgaven er å lage et egendesignet, symmetrisk bilde. Elevene kan dra i hjørnene til originalfigurene og endre farger. Legg merke til at det bare er figurene som er utgangspunktet for speilingene som er bevegelige.
Kommentarer til læreren
I oppgave 6.1 bruker elevene verktøyet Mangekant. Det kan være nødvendig å minne dem på at de må trykke på startpunktet for å avslutte figuren. Oppgave 6.2 er egnet som en innlevering enten digitalt eller som utskrift på papir.
Det er mulig å avslutte undervisningsopplegget etter at elevene har gjort oppgave 6.2 på Kikora sin plattform. Vi anbefaler imidlertid at elevene arbeider med samme tema og verktøy i det vanlige GeoGebra-programmet slik at de også lærer å bruke GeoGebra uten hjelpen som Kikora gir underveis. Et forslag finner du i aktivitet 4.
Aktivitet 4
I denne aktiviteten bruker elevene det de har lært om speiling og om verktøyene i GeoGebra. Elevene arbeider på hver sin PC i det vanlige GeoGebra-programmet. Da får de trening i å bruke programmet, i tillegg til at arbeidsfeltet er større og flere verktøy er tilgjengelige.
Læreren gir oppgaven muntlig eller skriftlig.
- Åpne GeoGebra.
- Skjul koordinatsystem og velg isometrisk rutenett

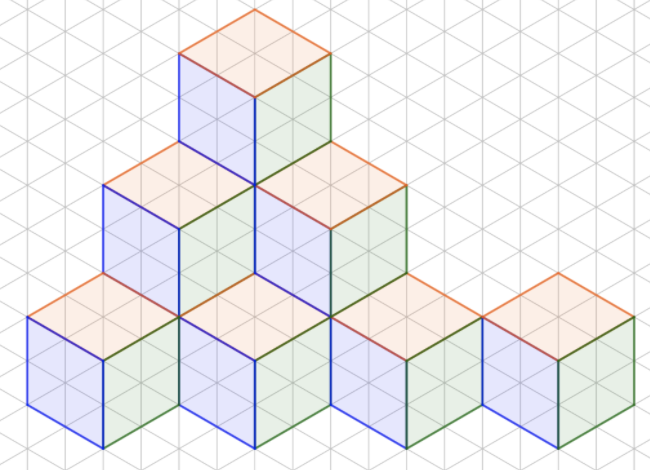
- Bruk Mangekant og tegn en rombe. Velg én eller to ruter som sidelengde.
- Lag en figur som består av mange terninger ved å speile om sidekanter.
- Fargelegg terningene med tre farger slik at figuren ser tredimensjonal ut.
Kommentarer til læreren
Oppgaven er ikke krevende, men gir et pent resultat. Rutenettet gjør det enkelt å tegne den første romben. Minn elevene på å bruke Flytt når de skal endre farge.
Noen elever vil kanskje prøve å lage terninger med parallellogram hvor to og to sider er like lange (ikke alle fire slik som for en rombe). Det fungerer fint når de speiler i en retning, men ikke hvis de speiler i alle retninger. Hvorfor?
Rammeplanmål/Kompetansemål
- Grunnskole
- Kompetansemål etter 6. trinn
- utforske og beskrive symmetri i mønster og utføre kongruensavbildingar med og utan koordinatsystem
- bruke variablar, lykkjer, vilkår og funksjonar i programmering til å utforske geometriske figurar og mønster
