Andregradsfunksjoner 2
Opplegget er en revidert versjon fra heftet Undersøkende matematikkundervisning i videregående skole.
Emne
Andregradsfunksjon, funksjonsuttrykk, graf, ekstremalpunkt, toppunkt, bunnpunkt, nullpunkt.
Hensikt
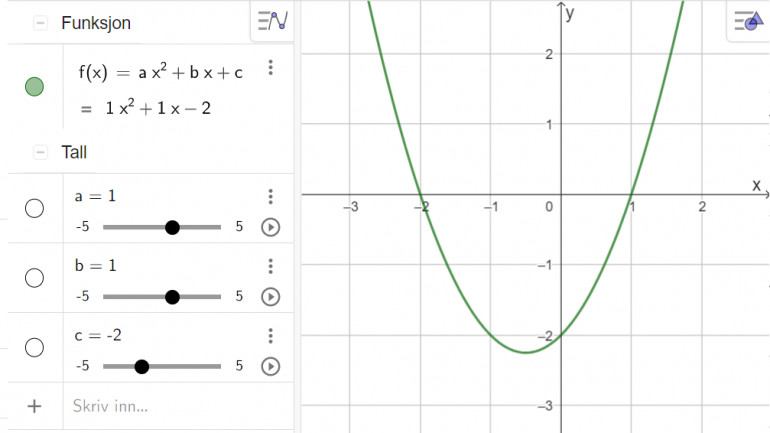
Elevene skal utforske sammenhengen mellom funksjonsuttrykk og graf ved å variere koeffisientene.
Valg av tidspunkt
Du trenger
PC med GeoGebra og elevark (Word).
Aktiviteten
Elevene skal bli kjent med hvordan koeffisientene til andregradsfunksjonen påvirker grafen. De bruker GeoGebra i utforskningen og arbeider parvis med hvert sitt elevark. Elevene bør skrive ned det de oppdager, både med ord og matematiske symboler. Oppfordre elevene til å bruke begrep som funksjonsuttrykk, graf, ekstremalpunkt, toppunkt, bunnpunkt, andregradskoeffisient, førstegradskoeffisient og konstantledd.
Prøv ut aktivitetene på forhånd slik at du vet hva elevene skal gjøre og hvilke problemer som kan oppstå, både faglige og tekniske. Minn elevene på å teste løsningene sine i GeoGebra.
Aktivitet 1-3
Elevene skal variere én og én koeffisient ved hjelp av glidere i GeoGebra. De skal observere og beskrive hvilke egenskaper til grafen som endrer seg og som ikke endrer seg. Målet er at de skal oppdage sammenhengen mellom funksjonsuttrykk og graf når koeffisientene varierer.
Kommentar til læreren
Sørg for at elevene kjenner til begrepene koeffisient og variabel. I uttrykket elevene skal arbeide med står koeffisientene a, b og c for ukjente tall som er faste, mens variabelen x står for et ukjent tall som kan variere.
Elevene kan ha nytte av å bruke sporing av punkter når de undersøker funksjonene. For eksempel ved å tegne ekstremalpunktet til funksjonen, høyreklikke på punktet og velge Vis spor. Når elevene beveger på en glider, vil GeoGebra tegne sporet til ekstremalpunktet. Det kan gjøre det lettere å beskrive hva som skjer.
Når alle elevene har skrevet ned sine observasjoner fra aktivitet 1, kan det være lurt med en klassesamtale for å komme fram til hva en god beskrivelse bør inneholde. Velg ut noen elevpar som presenterer sine beskrivelser, og bruk disse som utgangspunkt for samtalen. Ved å undersøke likheter og ulikheter til hverandres beskrivelser, kan elevene bli bedre til å beskrive matematiske observasjoner med egne ord.
Aktivitet 4
Elevene skal bruke erfaringene fra aktivitet 1-3 til å lage funksjoner som oppfyller gitte kriterier. Målet er at de skal få varierte erfaringer med andregradsfunksjoner.
Kommentar til læreren
I de fleste oppgavene skal elevene starte med å tegne en funksjon. Så skal de resonnere seg fram til hvordan de kan endre funksjonsuttrykket slik at grafen tilfredsstiller nye kriterier. Oppfordre elevparene til å lage hypoteser, resonnere og diskutere muntlig før de tester løsningene sine i GeoGebra. Elevene kan også lage oppgaver til hverandre.
Oppsummering
La elevene dele beskrivelsene fra aktivitet 1-3. Snakk også om utvalgte oppgaver fra aktivitet 4. Hvordan har elevene løst oppgavene og hvordan har de tenkt? På forhånd kan du gjerne spørre noen elevpar om å presentere løsningen sin og forklare hvordan de har tenkt.
Rammeplanmål/Kompetansemål
- Videregående
- Vg1P
- bruke digitale verktøy i utforsking og problemløysing knytt til eigenskapar ved funksjonar, og diskutere løysingane
- tolke og bruke funksjonar i matematisk modellering og problemløysing
- Vg1T
- utforske og beskrive eigenskapane ved polynomfunksjonar, rasjonale funksjonar, eksponentialfunksjonar og potensfunksjonar
- utforske samanhengar mellom andregradslikningar og andregradsulikskapar, andregradsfunksjonar og kvadratsetningane og bruke samanhengane i problemløysing
