Estimering

I dagligdagse situasjoner er det ofte ikke nødvendig å regne ut helt nøyaktig. Ofte er det godt nok med et estimat. Estimering handler om å anslå en ukjent størrelse, uten å vite det helt sikkert. Du anslår så godt du kan, basert på det du vet fra før og sunn fornuft. Tenk deg at du skal kjøre på ferietur. Du vet hvor langt du skal kjøre og vil beregne omtrent hvor lang tid det tar. Du foretar en vurdering av hva gjennomsnittsfarten kan være. Du vet at det kan være kø noen steder, noe som påvirker gjennomsnittsfarten. Det er kanskje behov for å ta en lengre pause for å lade bil eller spise litt på veien og du må legge til litt ekstra tid. Du gjør en omtrentlig beregning av hvor lang tid det kan ta.

Eksemplet over og andre dagligdagse situasjoner er en god inngang til å arbeide med estimering. Det inviterer elevene til å ta i bruk egne erfaringer og kjente mengder, antall og størrelser for å gjøre et estimat. Det er fint for elevene å få mulighet til å reflektere over når det er nødvendig å regne nøyaktig og når det er greit nok med et overslag. Språket vi bruker, kan bidra til å forstå estimering bedre. Ord som cirka, omtrent, litt mer/mindre, nesten og mellom, støtter opp om å gjøre estimeringer.

Det er vanlig å skille mellom fire ulike typer estimering.

1. Estimering av antall

Å estimere antall handler om å tallfeste antall elementer i en mengde uten å ty til telling. Det er en sammenheng mellom elevenes ferdighet i telling og hvor nøyaktig de gjør et estimat. Ikke så uventet kanskje, men estimatet blir mindre nøyaktig når antall elementer i mengden øker. (Sunde et al., 2022)

Typiske oppgaver for å estimere antall er oppgaver hvor elevene skal anslå hvor mange prikker det er på et bilde eller estimere antall plastfigurer i en krukke.

2. Estimering på tallinja

Det er nær sammenheng mellom elevenes estimering på tallinja og deres matematiske forståelse. Tallinja er en sentral representasjon for å vise tallstørrelser. Det å si hvilket tall som er merket av på tallinja eller å plassere et tall på tallinja, viser hvilken forståelse for tall elever har (Schneider et al., 2018).  

Den tidlige oppfattelsen av tallinja er basert på logaritmisk tenking. Det kommer til uttrykk ved at små tall blir oppfattet som langt fra hverandre og større tall nærmere hverandre (Figur 1). Etter hvert som elever får bedre tallforståelse, blir oppfattelsen mer lineær. Det er like langt fra 10 til 20, som fra 80 til 90 (Figur 2).

Eksemplene nedenfor viser et tenkt tilfelle av hvordan elever som har en logaritmisk og lineær oppfattelse av tallinja plasserer tallene 1,10, 20, 35, 60, 70 og 90.

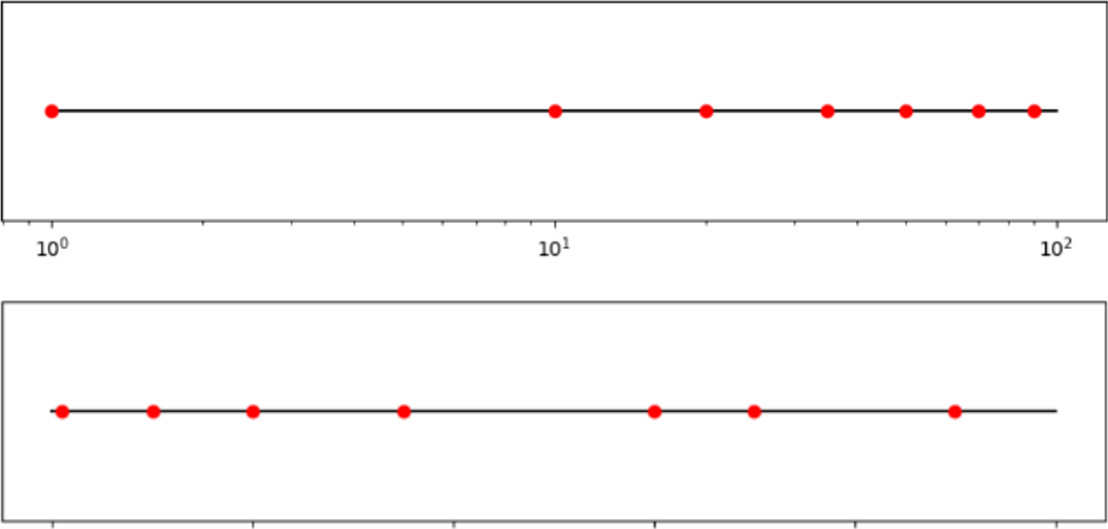
I overgangen fra logaritmisk til lineær oppfattelse av tallinjen er det noen milepæler. I begynnelsen forholder elevene seg bare til startpunktet, men etter hvert bruker de i tillegg sluttpunktet til å vurdere hvilket tall som er merket av eller hvor de skal plassere et tall. Den siste milepælen mot en lineær oppfattelse av tallinje er når de i tillegg vurderer opp mot et midtpunkt, da blir plasseringen mer nøyaktig (Schneider et al., 2018).

3. Estimering ved utregning

Estimering ved utregning defineres som en prosess for å forenkle en utregning ved å bruke regler og prosedyrer til å komme fram til et omtrentlig, men samtidig tilfredsstillende svar ved hjelp av hoderegning (Ainsworth et al., 2002).

En praktisk situasjon som inviterer elevene til å estimere ved utregning, kan være å planlegge påskelunsj. Hvor mange brød trengs? Hvilke typer pålegg og hvor mye av hver sort? Hvor mange liter drikke? Hva om det skal kokes kakao, hvor mye av hver ingrediens trengs? En annen situasjon er å finne hvor mange kroner rabatt du får, når en vare er satt ned med 25 %. Begge disse to situasjonene er eksempler på dagligdagse situasjoner hvor det vil være godt nok å gjøre en estimering.  

4. Estimering av størrelser (lengde, volum, masse, tid etc.)

For å anslå størrelsen til noe uten å bruke måleinstrumenter, kan elevene bruke ulike mentale referanser. Dette gjelder i dagligdagse situasjoner hvor konteksten gjør at det ikke er nødvendig med eksakte mål eller at det er umulig å gjennomføre nøyaktige målinger (Sunde et al., 2022).

Fire strategier kan være nyttige for å estimere størrelser (Van de Walle, 2010):

1. Utvikle og bruke referansepunkter for å estimere. Referansepunkter er størrelser som elevene har et forhold til. F.eks. egen høyde eller at en melkekartong inneholder 1 L.
2. Vurdere delelementer i størrelsen man skal estimere. Det er enklere å vurdere høyden til en bokstabel, om man kan anslå at tykkelsen til en bok er cirka 2 cm. Å anslå lengden til en vegg med vindu kan gjøres ved at man anslår bredden til vinduet og bruker det som utgangspunkt for å anslå lengden til hele veggen.
3. Dele opp i mindre enheter. Det som skal måles kan halveres helt til man har en enhet som lar seg vurdere og deretter multiplisere opp. Se for deg en vegg uten dører eller vinduer. Da kan du mentalt halvere lengden til veggen til du har en enhet du kan anslå lengden til og deretter anslå lengden til veggen.
4. Gjenta en enhet enten mentalt eller fysisk. For eksempel kan lengden på foten eller skrittlengde brukes til å måle lengden på for eksempel klasserommet. Et annet eksempel er å vurdere hvor mange melkekartonger det er plass til i en vaskebøtte, ved å se for seg hvor mange det er plass til i bøtten.

Å anslå vekt til et gresskar, høyden til flaggstang og volum i et melkeglass er eksempler på praktiske situasjoner hvor elevene kan estimere størrelse.

Det ligger i sakens natur at man ikke får nøyaktig svar når man gjør en estimering. Et estimat er hverken riktig eller feil, men innenfor et akseptabelt intervall. Elever er ofte vant til at matematikk gir riktige svar og kan bli frustrerte når det ikke finnes et fasitsvar. Å estimere kan motvirke fokuset på å finne ett riktig svar og trigge elevene til å vurdere hva som kan være rimelige svar. Estimering bidrar til at elever utvikler evnene til å stille kritiske spørsmål til egne og andres resonnement.

Referanser

Ainsworth, S., Bibby, P., & Wood, D. (2002). Examining the effects of different multiple representational systems in learning primary mathematics. The Journal of the Learning Sciences, 11(1), 25-61.

Schneider, M., Merz, S., Stricker, J., De Smedt, B., Torbeyns, J., Verschaffel, L., & Luwel, K. (2018). Associations of number line estimation with mathematical competence: A meta‐analysis. Child Development, 89(5), 1467-1484.

Sunde, P. B., Petersson, J., Nosrati, M., Rosenqvist, E., & Andrews, P. (2022). Estimation in the mathematics curricula of Denmark, Norway and Sweden: Inadequate conceptualisations of an essential competence. Scandinavian Journal of Educational Research, 66(4), 626-641.

Van de Walle, J. A. (2010). Elementary and middle school mathematics : teaching developmentally (7th ed. ed.). Allyn and Bacon.