Tallgjenkjenning og representasjoner

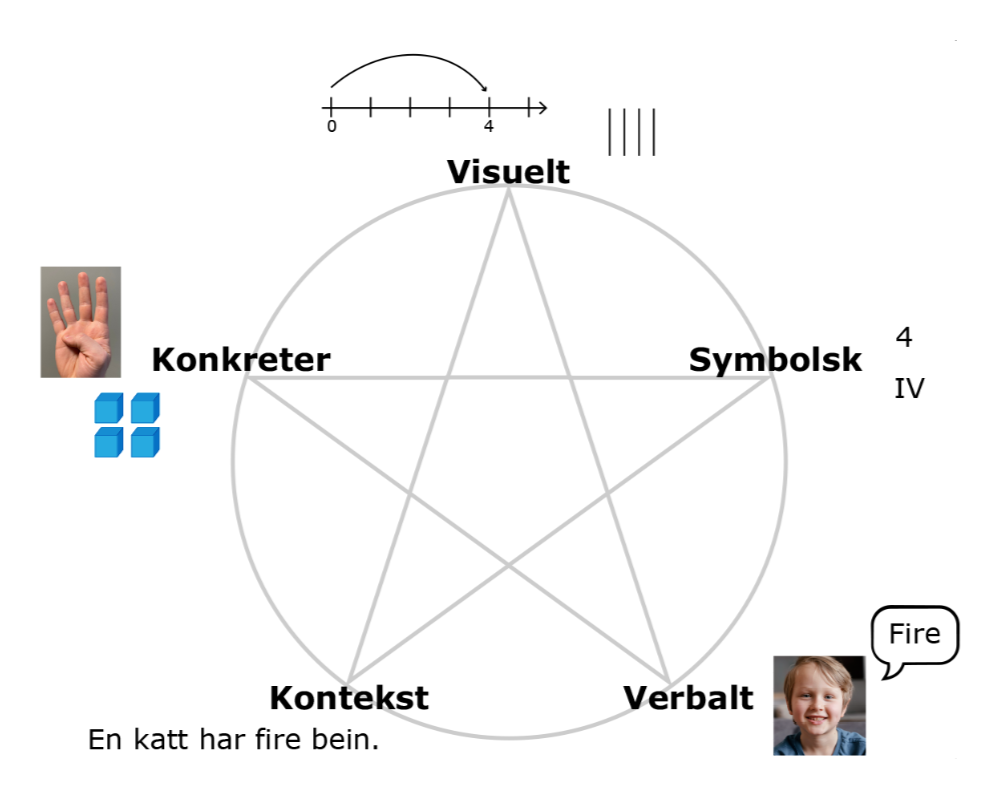
Tall og regneoperasjoner er abstrakte matematiske begreper, og de må representeres på en eller annen måte. Kjerneelementet «Representasjon og kommunikasjon» i LK20 peker på fem ulike typer representasjoner: konkrete, kontekstuelle, visuelle, verbale og symbolske (Kunnskapsdepartementet, 2020). Mengden 4 kan representeres konkret med fire elementer (tellebrikker, fingre etc.), kontekstuelt ved å vise at en katt har fire bein, visuelt på tallinja, verbalt ved å si ordet «fire» og symbolsk med symbolet «4». 

Tallgjenkjenning handler om å kjenne igjen tall uavhengig av hvilken representasjon vi bruker.

Symbolsk representasjon

Symbolsk representasjon i matematikk innebærer bruk av matematiske symboler og notasjoner for å uttrykke tall og operasjoner.

Tallet fire blir representert symbolsk som «4». Om vi skal legge sammen tallene 19 og 6, så blir det representert symbolsk som «19 + 6».

Symbolske representasjoner er en effektiv representasjonsform som gjør det mulig å si mye ved å bruke få tegn. Symboler er dog en abstrakt representasjonsform, så det matematiske begrepet som blir representert er ikke nødvendigvis tilgjengelig for elevene dersom de kun møter symbolske representasjoner. Elevene er altså avhengige av god begrepsmessig forståelse og mye erfaring med de matematiske begrepene før symbolene blir tilgjengelige for dem.

Visuell representasjon

Visuell representasjon er tegninger eller bilder på begreper, situasjoner eller operasjoner. Visuelle representasjoner kan være uformelle, slik som matematiske tegninger, tellestreker og prikker, til mer standardiserte visuelle representasjoner, slik som tallinjer, rutenett og, diagrammer.

Tallinja er en mye brukt visuell representasjon. Tallinja kan både være en representasjon av ett eller flere tall, men også brukes som en modell, eller verktøy, for å gjøre en prosedyre. Særlig i addisjon og subtraksjon kan tallinja være til nytte for å utføre prosedyrer.

Når vi for eksempel representerer tallet 4 på tallinja, kan det se slik ut:

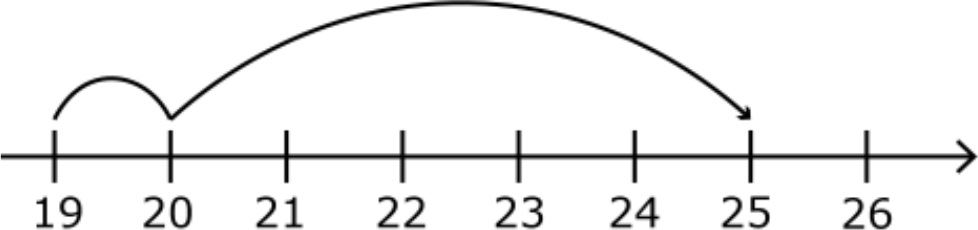
Når vi bruker tallinja som verktøy for å regne ut et regnestykke, kan det for eksempel se slik ut for regnestykket 19 + 6:

Visuelle representasjoner hjelper elevene å utvikle forståelse for de matematiske begrepene og prosedyrene. (NCTM). Visuelle representasjoner vil også kunne støtte elever med andre morsmål og elever som trenger tilrettelagt undervisning ettersom de visuelle representasjonene tillater flere elever å kommunisere matematisk (Fuson & Murata, 2007).

Kontekstuell representasjon

Kontekstuell representasjon i matematikk innebærer å bruke virkelighetsnære situasjoner eller historier for å illustrere matematiske begreper og operasjoner.

For eksempel kan tallet fire bli representert med at en katt har 4 bein eller at en bil har 4 dekk. Regneoperasjonen 19 + 6 kan for eksempel bli representert ved en regnefortelling som «Hvor mange drops har vi til sammen om vi har 19 drops i én pose, og 6 drops i en annen pose?»

For at matematikken skal bli tilgjengelig for elevene utenfor klasserommet, er det viktig at de får øving i å arbeide i kontekst. Ved å få erfaring i å bruke kontekstuelle representasjoner vil elevene kunne bruke sin uformelle matematikkompetanse i og utenfor klasserommet. Dessuten kan kontekst ofte påvirke både grad av nøyaktighet som kreves og hvilke strategier som brukes i oppgaver elevene arbeider med.

Verbal representasjon

Verbal representasjon i matematikk innebærer å bruke det muntlige språket for å beskrive matematiske begreper, operasjoner, strategier og løsninger.

Når barn teller til fire, teller de ofte høyt «én to tre fire», og kan blande sammen det å telle høyt med selve tallet 4. Om den voksne spør: «Hvor mange har du da?», kan det ofte avdekkes om barnet svarer «fire» eller sier «én to tre fire» på nytt.

Når et barn forklarer hvordan han løste regnestykket 19 + 6 ved å si at «Jeg tok én over fra nitten til seks og la sammen tjue og fem», så bruker barnet verbal representasjon for å beskrive en strategi for å løse regneoperasjonen 19 + 6.

Elevene trenger å møte utfordringer som krever et behov for å bruke språket presist i matematikk. Da får de trening i å uttrykke seg muntlig slik at de er bedre rustet både til å beskrive begrep, begrunne strategier eller forklare løsninger. Dersom det muntlige språket i matematikken utvikles tidlig, får både elevene sterkere forståelse av tallene tidlig, og de blir bedre vant til å uttrykke seg muntlig senere.

Konkret representasjon

Konkret representasjon i matematikk innebærer bruk av fysiske objekter for å illustrere matematiske begreper og operasjoner. Dette kan også være bruk av fingrene.

Å holde opp fire fingre er en representasjon av tallet fire. Operasjonen 19 + 6 kan illustreres med tellebrikker. Noe konkretiseringsmateriell viser tiere og enere, og man kan da bruke enerne til å bygge en ny tier, og da se at vi har to tiere og fem enere.

Mennesker oppfatter verden og lærer ved å bruke sansene. Å ta i bruk noe konkret både for å lære, men også for å kommunisere, er altså veldig naturlig for oss. For eksempel er noe så enkelt som å telle på fingrene et nyttig verktøy når elever skal få bedre forståelse av tallene. Ved bruk av konkreter vil ofte både de matematiske begrepene og problemstillingene bli mer tilgjengelige for elevene. De kan bruke konkreter både som et redskap og som et språk. Konkretiseringsmateriell, som for eksempel fingertelling, kan være et språk som hjelper elevene i tenkingen (Johnsen Høines, 1998).

Variert bruk av representasjonstypene

Ovenfor er de fem representasjonstypene beskrevet. For at elevene skal kunne utvikle god tallforståelse, må de få muligheten til å bruke forskjellige representasjonsformer, og kunne oversette mellom dem (Niss & Jensen, 2002). Å representere tall symbolsk er altså ikke tilstrekkelig. Et tegn på god begrepsforståelse i matematikk er at en kan representere et matematisk objekt på flere ulike måter (Enge & Valenta, 2013). Det er likevel ikke alltid hensiktsmessig å representere matematiske begreper med alle representasjonstypene. Av og til kan det være tilstrekkelig å arbeide med to og andre ganger flere ulike typer (Valbekmo et al., 2019). 

Referanser

Andrews&Sayers

Læreplanen

Valbekmo et al

Enge og Valenta

Johnsen Høines, Begynneropplæringen (1998)

Niss&Jensen

NCTM – Principles to action

Fuson, Karen C., and Aki Murata. “Integrating NRC Principles and the NCTM Process

Standards to Form a Class Learning Path Model That Individualizes within Whole-

Class Activities.” National Council of Supervisors of Mathematics Journal of Mathe-

matics Education Leadership 10, no. 1 (2007): 72–91