GeoGebra og kjerneelementene

Det digitale verktøyet GeoGebra blir mye brukt i norske klasserom, og i tiden framover vil fokuset på bruk av digitale verktøy i skolen øke ytterligere (Kunnskapsdepartementet, 2017). GeoGebra kan gi elevene muligheter til å utforske matematiske ideer og sammenhenger og å bruke erfaringene de har fått, til å utvikle en fleksibel og robust forståelse av matematikk. I læreplanen (LK20) står det i kompetansemålene etter 6. trinn at elevene skal «utforske og beskrive symmetri i mønster og utføre kongruensavbildningar med og utan koordinatsystem» (Utdanningsdirektoratet, 2019). Elevene kan utvide sin forståelse av de tre kongruensavbildningene speiling, rotasjon og parallellforskyvning ved å bruke GeoGebra til å utforske de geometriske sammenhengene. Programmet har egne verktøy for de tre kongruensavbildningene, og i denne artikkelen ser vi på rotasjon.

I tradisjonell geometriundervisning lærer elevene hvordan de skal rotere figurer, før de får i oppgave å gjøre det selv med papir og blyant. I GeoGebra kan vi snu denne prosessen slik at elevene selv kan oppdage hva som skjer når de roterer en figur. Målet med opplegget er at elevene skal bli kjent med egenskapene til rotasjon. De skal utvikle forståelse for hva som skjer når vi roterer et objekt, hva som kjennetegner et rotasjonssymmetrisk objekt, hvordan de finner rotasjonssenteret til en slik figur, hva rotasjonsvinkel er, og hvordan de finner rotasjonsvinkelen. Fra før kjenner elevene på 6. trinn til ulike todimensjonale figurer og deres egenskaper (vinkler, kanter og hjørner), men noen kan trenge en oppfriskning. De må også kunne tegne likesidede/regulære mangekanter, måle vinkler og lage glidere i GeoGebra.

Utforsking av rotasjon

Undervisningsopplegget starter med at vi viser en animasjon av en trekant som roterer om et punkt. Fokuset skal være på rotasjon som kongruensavbildning (formen er bevart etter rotasjon) og hva som skjer med hjørnene til figuren under rotasjonen. Animasjonen heter Rotasjon (se Figur 1), og vi finner den her (eller lager den selv). Det er mulig å bevege på glideren for å rotere figuren samt rotere automatisk med start- og stoppknappen. GeoGebra kan vise originalfiguren og rotasjonsvinkelen, i tillegg til den roterte figuren. Det gjør det lett å se at 360° er en hel omdreining siden den roterte figuren dekker originalfiguren. I animasjonen er det satt på sporing på hjørnene slik at elevene kan følge bevegelsen til punktene. Ved å stoppe animasjonen, dra i et hjørne eller flytte hele figuren og så starte animasjonen igjen flere ganger, får elevene varierte erfaringer med rotasjon. Vi lar elevene bestemme hvilke endringer vi gjør og vi lar de prøve å forutse hva som kommer til å skje. Samtidig passer vi på å få undersøkt hva som skjer når rotasjonssenteret er utenfor, på og innenfor figuren.

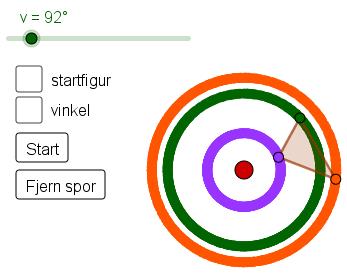
Så diskuterer vi i helklasse hva vi har sett. Hvorfor tegnes det sirkler? Hva betyr tallene på glideren? Hvor ligger figuren hvis glideren står på 90° eller 180°? Her kan det også være lurt å spørre om hva som skjer når man roterer med 360°, 540° eller 720°. Disse vinklene er godt kjente for elever som liker snowboard eller skateboard, noe som gjør det lettere å knytte rotasjon til noe de kan fra før. Og hvor er vinkelen GeoGebra måler? Ved å klikke på vinkel i animasjonen kommer to linjestykker mellom punkt på originalfiguren, rotasjonssentrum og punkt på den roterte figuren fram, i tillegg til vinkelen mellom linjestykkene (se Figur 2). Vinkelen vokser i takt med glideren, men starter på nytt etter 360°. Hvorfor gjør den det?

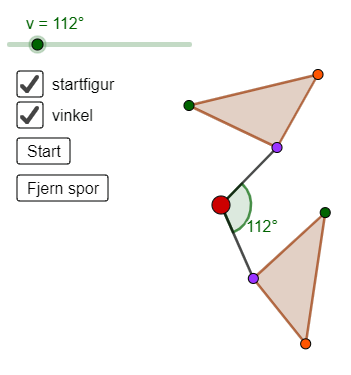
Etter klassediskusjonen arbeider elevene videre i par eller små grupper med å utforske likesidede mangekanter i GeoGebra. Elevene skal finne ut hvor mange grader de må rotere mangekanten for å få den roterte figuren til å dekke originalfiguren. Må de alltid rotere 360°, eller er det mulig å rotere med en mindre vinkel? Elevene vil oppdage at plasseringen av rotasjonssenteret er avgjørende for at de skal kunne dekke originalfiguren ved å rotere med en vinkel som er mindre enn 360°.

Elevene starter med en ny GeoGebra-fil. Vi skal kun vise elevene ikonet for Rotasjon og hvordan de bruker det. Elevene får så utlevert et ark med en likesidet sekskant, et kvadrat og en likesidet trekant (se Figur 3). Det er viktig at elevene får prøve (og feile) uten at vi kommer med løsningene. Elevene har lært nok om rotasjon til at de kan klare å løse oppgavene, og jo mer elevene får prøve selv, jo bedre blir de til å bruke GeoGebra. Det digitale verktøyet hjelper elevene med å utvide forståelsen av geometri, og elevene opplever også opplæringen i det digitale verktøyet som relevant når den skjer samtidig som de arbeider med matematiske problemer (Stengrundet, 2019).

Rekkefølgen på oppgavene er valgt bevisst. Elevene ser sammenhengen med vinkler bedre i en sekskant enn i en trekant. Det er også enklere å finne midtpunktet i mangekanter hvor antall sider er et partall enn et oddetall, så det å starte med for eksempel en femkant vil ødelegge mye av eksperimenteringen.

Vi går rundt og observerer hvordan elevene angriper problemet. Tenker elevene før de velger en verdi for vinkelen, eller prøver de seg bare fram? I motsetning til konstruksjoner på papir gjør GeoGebra det mulig å tegne alle mulige regulære mangekanter og velge alle mulige vinkelstørrelser. Elevene ser med en gang om løsningen stemmer. Angre-knappen gjør det lett å prøve på nytt hvis resultatet ikke blir som forventet.

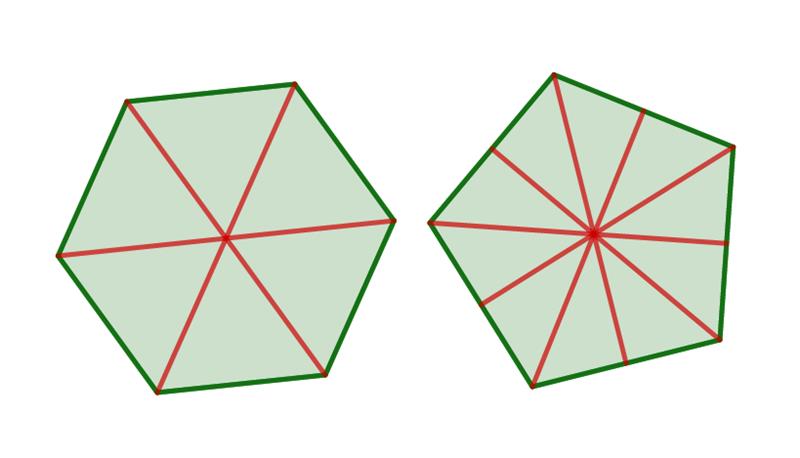
Elevene løser problemet ved utforsking. Først må de finne ut hvilken betydning plasseringen av rotasjonssenteret har, og hva som skjer når de roterer med ulike vinkler. Deretter må de diskutere og resonnere seg fram til hvorfor akkurat disse vinklene fungerer når rotasjonssenteret er plassert i midten av mangekanten. Etter å ha argumentert for løsningene sine, skal de finne en generell regel som gjelder for alle likesidede mangekanter når rotasjonssenteret er plassert i midten av figuren. Elevene vil også oppdage at det er enklere å finne midtpunktet hvis antall sider i mangekanten er et partall enn et oddetall (se Figur 4). Hvorfor er det slik?

Når elevene skal finne fram til matematiske sammenhenger ved prøving og feiling, er det avgjørende at vi som lærere er trygge på verktøyknappene elevene kan komme til å bruke i GeoGebra, og at vi har tenkt gjennom hva som kan skje i utforskingsprosessen. Vi skal ikke gi elevene løsningene ved å forklare hvordan de skal tenke, men i stedet legge til rette for at elevene kan starte med et enkelt problem før de løser mer komplekse oppgaver. Målet er at elevene kan finne rotasjonssentrum og rotasjonsvinkel til en hvilken som helst likesidet mangekant.

Som oppsummering skal elevene vise fram hvordan de har tenkt, og hvilke matematiske sammenhenger de har funnet. Vi velger ut elever som skal presentere arbeidet sitt basert på observasjonene vi har gjort underveis. Det er viktig å velge ut elever som har brukt forskjellige løsningsmetoder. Vi passer samtidig på å forklare og ta i bruk relevante matematiske begreper som rotasjonssymmetrisk, rotasjonssentrum og rotasjonsvinkel.

Bruk av kjerneelementene

I dette undervisningsopplegget bruker elevene GeoGebra til utforsking og problemløsning. Elevene leter etter mønster og sammenhenger, og strategiene er i fokus. Mens de arbeider, blir de introdusert for nye verktøy i GeoGebra, noe som bidrar til å øke elevenes problemløsningskompetanse. Animasjonen er en matematisk modell som elevene må tolke og anvende i utforskingen. Elevene må bruke resonnering og argumentasjon når de utvikler strategier, diskuterer, tenker gjennom hva som kommer til å skje etter at noen endringer er gjort, og presenterer løsningene sine. De må også forstå andre elevers resonnementer. Representasjon og kommunikasjon kommer til uttrykk gjennom at elevene må bruke matematiske begreper når de snakker matematikk. De må være presise når de forklarer hvordan de tenker, og hvorfor de mener at det er riktig. Elevene abstraherer og generaliserer når de går fra å løse et konkret problem med en sekskant til å løse et problem med en n-kant. De oppdager sammenhengene selv og formaliserer sammenhengene ved bruk av hensiktsmessige representasjoner. Det matematiske kunnskapsområdet i dette opplegget er geometri, og elevene utforsker rotasjon på varierte måter for å skaffe seg innsikt i egenskapene til rotasjon.

Alle kjerneelementene er sentrale når undervisningen foregår slik vi presenterer det i dette undervisningsopplegget, og det gir elevene et godt utgangspunkt for dybdelæring i matematikk. 

Referanser

Kunnskapsdepartementet (2017). Framtid, fornyelse og digitalisering: Digitaliseringstrategi for grunnopplæringen 2017-2021. Oslo: Kunnskapsdepartementet.

Stengrundet, S. (2019). Resonnering med GeoGebra. Hentet fra http://realfagsloyper.no/ (08.08.2019).

Utdanningsdirektoratet. Læreplanverket (www.udir.no/laring-og-trivsel/lareplanverket/)