Utforsking med Penn i GeoGebra

Verktøyet Penn lar elevene tegne i Grafikkfeltet (se ikon i figur 1). De kan bytte farge, utseende og tykkelse på tegningene (pennestrøkene) i Stilmenyen slik som for andre GeoGebra-objekter. Ved å holde inne høyre museknapp kan de også viske ut dersom noe ble feil. GeoGebra lagrer tegningene som skisser som elevene for eksempel kan flytte, rotere og speile.

Når elevene skal utforske matematiske sammenhenger i GeoGebra, er Penn nyttig for å markere relevante posisjoner. Elevene kan tegne oppå eksisterende objekter, for eksempel et punkt, og deretter flytte på objektet uten at markeringen følger med. Det er spesielt praktisk når elevene utforsker geometri. Merk at GeoGebra lagrer ikke koordinatene ved bruk av Penn. Hvis elevene trenger koordinatene til markeringene, må de bruke Punkt i stedet. Da kan de imidlertid ikke markere oppå andre objekter uten at punktet henger seg på. 

For å vise hvordan du kan bruke verktøyet i klasserommet, har jeg valgt ut tre aktiviteter. Alle tar utgangspunkt i at elevene lager en egen figur som de bruker som utgangspunkt for utforsking.

Trekanter med samme areal 

Varierte erfaringer er viktig for at elevene skal utvikle en robust og fleksibel forståelse av matematikk. I et dynamisk matematikkprogram som GeoGebra, kan elevene se mange eksempler basert på én dynamisk figur. For eksempel kan elevene lage en trekant med verktøyet Mangekant, og deretter dra i hjørnene for å lage uendelig mange eksempler på trekanter. Men hva om trekanten for eksempel skal ha areal 23? Ved å dra i et eller flere av hjørnene til den samme trekanten kan elevene finne en trekant som har areal 23. Og ved å fortsette slik kan de finne flere. Sørg gjerne for at elevene velger 0 eller 1 desimal som innstilling i GeoGebra. 

På jakt etter en matematisk sammenheng, vil elevene raskt få behov for å finne en systematisk måte å utforske trekanten. Å undersøke ett punkt om gangen er en nyttig strategi. Ved å bruke Penn for å markere posisjoner hvor arealet til trekanten er 23, kan elevene oppdage et mønster (figur 2). 

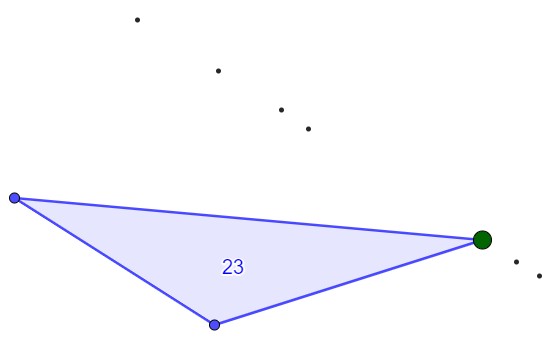
I begynnelsen vil elevenes bevegelser være vilkårlige, men etter hvert vil de bruke tidligere observasjoner til å forutse hvor de tror at punktet må være for at arealet skal bli 23. Erfaringene kan danne grunnlag for å lage en hypotese. De fleste vil oppdage at punktene ligger på linje. Noen vil også oppdage at linjen ser ut til å være parallell med den ene trekantsiden. Når elevene har laget en hypotese, kan de bruke verktøyene i GeoGebra til å teste om hypotesen stemmer. For eksempel kan de lage en rett linje gjennom markeringene, og deretter lage en ny trekant som har et punkt på linjen (grønn trekant på figur 3).

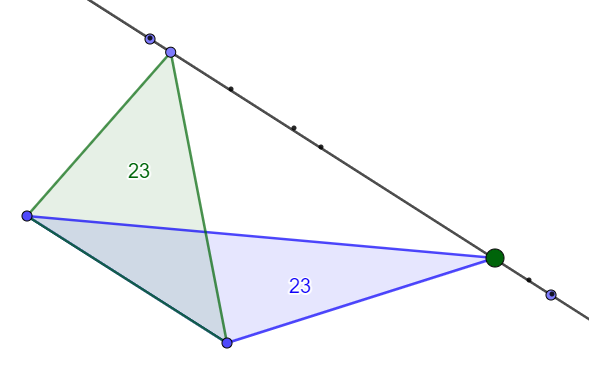
Etter at elevene har utforsket i GeoGebra, er det viktig med en matematisk klassesamtale for å oppsummere hva elevene har funnet ut. La dem dele observasjoner og hypoteser:

• Hva har elevene oppdaget?
• Hva er felles for trekantene med areal 23? Hva er forskjellig?
• Hvorfor blir arealet 23?

Dette gir en god anledning til å snakke om sammenhengen mellom grunnlinje, høyde og areal i trekanter.

Trekanter med en rett vinkel 

Elevene kan også bruke en trekant som utgangspunkt for å utforske rettvinklede trekanter. De starter igjen med å lage en vilkårlig trekant med Mangekant. Klarer de å bevege på trekanten slik at en av vinklene blir 90º? Kan de finne en ny trekant hvor den samme vinkelen fortsatt er 90º? Kan de finne flere slike trekanter? Elevene markerer posisjonene som tilfredsstiller kriteriet med Penn, og etter hvert kan observasjonene gi et utgangspunkt for å lage hypoteser. 

Avhengig av hvilket punkt elevene beveger på, vil de oppdage ulike mønster. For de som beveger et punkt som ikke er toppunkt til den rette vinkelen, vil det se ut som om punktet må ligge på en normal linje til den ene trekantsiden (figur 4). Elevene kan teste om det stemmer ved å lage den normale linjen og en ny trekant.

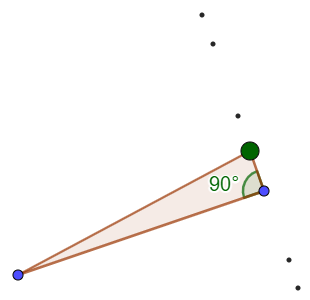
For de som beveger på toppunktet til den rette vinkelen, vil det se ut som om punktet ligger på en halvsirkel over den motstående trekantsiden (figur 5). Ved å lage halvsirkelen og en ny trekant kan elevene se om vinkelen alltid blir 90º.
 

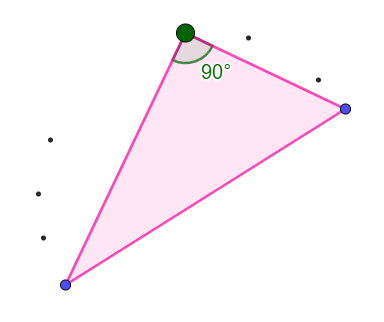
Disse observasjonene kan også være et godt utgangspunkt for en klassesamtale, slik at elevene kan dele observasjoner og hypoteser. De kan teste hypotesene sine ved å lage dynamiske, rettvinklede trekanter i GeoGebra ved hjelp av en normal linje eller en halvsirkel. At en trekant blir rettvinklet hvis de bruker en normal er nok kjent for de fleste elevene. Varianten med halvsirkel vil antakeligvis være en ny oppdagelse for mange. Sammenhengen heter Tales’ halvsirkelteorem. 

Her er en film som viser bruk av Penn til denne aktiviteten: 

Rektangler i et rektangel

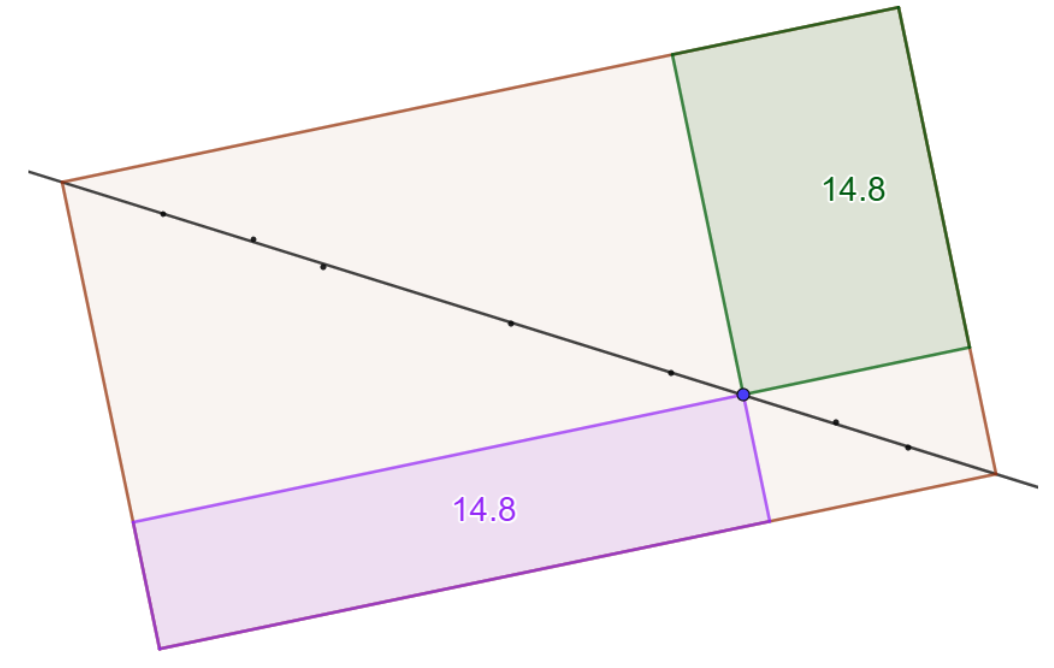
Rektangler i et rektangel er et godt utgangspunkt for både utforsking og bevis. Elevene lager først et dynamisk rektangel i GeoGebra. Deretter lager de et punkt i rektangelet, og bruker Parallell linje og Mangekant til å tegne rektanglene (figur 6, lilla og grønt) inni det store rektangelet. Elevene kan så undersøke om det er mulig å bevege punktet slik at lilla og grønt rektangel har like stort areal. Noen vil tenke at det bare er én mulig løsning, nemlig midtpunktet til det store rektangelet, mens andre vil prøve vilkårlig. Etter hvert vil de oppdage at punktet må ligge på diagonalen til det store rektangelet.

Observasjonene fra utforskingen kan støtte elevene i arbeidet med å bevise sammenhengen. Hva er det som er spesielt med figuren når punktet ligger på diagonalen? Oppfordre elevene til å tegne diagonalen og studere hvordan den deler det store rektangelet. 

Oppsummering 

De tre eksemplene viser hvordan elevene kan oppdage geometriske sammenhenger med god støtte av Penn-verktøyet. Utgangspunktet kan være en enkel figur som en trekant, eller mer avanserte figurer, avhengig av elevenes GeoGebra-kompetanse. Å bruke Penn kan gjøre det lettere for elevene å få et visuelt bilde av observasjonene sine, og deretter lage en hypotese. Det er viktig å poengtere for elevene at selv om hypotesen stemmer når de tester den i GeoGebra, så er det ikke et bevis for den matematiske sammenhengen. Slike oppdagelser kan imidlertid gjøre at elevene blir nysgjerrige og har lyst til å bevise sammenhengene selv. 

Referanser

Brunström. M. (2015). Matematiska resonemang i en lärandemiljö med dynamiske matematikprogram. Karlstad University Studies.