Har dine elever utforsket med GeoGebra?

GeoGebra kan gi elevene mulighet til å utforske matematiske sammenhenger på en helt annen måte enn med papir og blyant. Ved å lage og bevege dynamiske figurer kan elevene undersøke mange utgaver på kort tid. Varierte erfaringer er viktig for å utvikle en fleksibel og robust forståelse av matematikk. La elevene lage figurene i GeoGebra selv. Det er vel anvendt tid!
Hva sier læreplanen?
Den nye læreplanen LK20 vektlegger utforsking i større grad enn tidligere læreplaner; utforsking inngår i kjerneelementet Utforsking og problemløsing, og skal prege all undervisning i matematikk. I tillegg er det et av de mest brukte begrepene i kompetansemålene. Det står for eksempel at elevene skal:
- «utforske, teikne og beskrivegeometriske figurar …» (2. trinn)
- «utforske, beskrive og samanlikne eigenskapar ved to- og tredimensjonale figurar ved å bruke vinklar, kantar og hjørne» (4. trinn)
- «utforskeog beskrive symmetri i mønster og utføre kongruensavbildingar …» (6. trinn)
- «Utforskeeigenskapane ved ulike polygonar og forklare omgrepa formlikskap og kongruens» (9.trinn)
Utforsking er også en del av Digitale ferdigheter hvor det står at elevene skal «bruke og velje formålstenlege digitale verktøy som hjelpemiddel for å utforske, løyse og presentere matematiske problem». Læreplanen legger derfor godt til rette for å bruke de dynamiske egenskapene til GeoGebra til utforsking.
GeoGebra for alle trinn!
Hva vil det si å utforske med GeoGebra? I GeoGebra kan elevene lage figurer basert på matematiske egenskaper. De kan lage statiske figurer. For eksempel en trekant som alltid har sidene 4, 6 og 9. Eller dynamiske figurer som de kan bevege på samtidig som figurene beholder gitte egenskaper. For eksempel en trekant som er likebeint uansett hvordan de drar i figuren eller firkant som alltid er et rektangel. Å lage og bevege slike dynamiske figurer kan være et godt utgangspunkt for å utforske matematikk.
I GeoGebra er det lett å tilpasse utforskingen til ulike trinn. Elever på barnetrinn kan for eksempel utforske arealet til en trekant med kjent grunnlinje og det tredje hjørnet på en parallell linje (til grunnlinjen), mens elevene på ungdomstrinnet kan kombinere kunnskapen med algebra for å lage trekanter som alltid har et gitt areal.
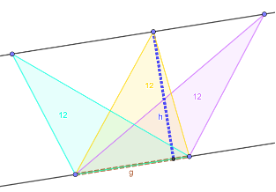
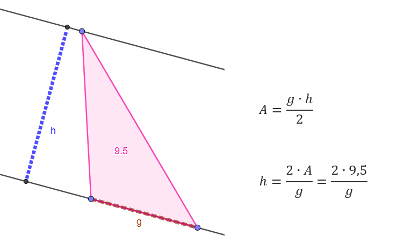
De første gangene elevene skal lage egne dynamiske figurer vil de bruke en del tid til selve konstruksjonen. De må bruke flere verktøy og huske å aktivere Flytt før de kan bevege figuren. Det kan være fristende å spare tid ved å gi elevene ferdige, dynamiske figurer, men Brunström (2015) har vist at elever som begynner med blanke ark i GeoGebra, lager hypoteser raskere og er mer utholdende i utforskingsprosessen. Tiden det tar å la elevene lage egne figurer er derfor vel anvendt tid.
Har du lyst til å prøve deg? Her finner du læringsressursene vi har utviklet for GeoGebra
Denne artikkelen er en bearbeidet versjon av "Utforske matematikk med dynamisk geometri" som stod på trykk i Tangenten nr. 3/2021.
Kilder
Brunström. M. (2015). Matematiska resonemang i en lärandemiljö med dynamiske matematikprogram. Karlstad University Studies.

