Å kunne regne i naturfag

Dette sier læreplanen
Å kunne regne i naturfag er å kunne innhente, bearbeide og framstille relevant tallmateriale. Regning i naturfag innebærer å bruke begreper og velge passende måleinstrumenter, måleenheter og formler for å løse naturfaglige problemstillinger. Regning i naturfag er også å kunne sammenligne, vurdere og argumentere for om beregninger, resultater og framstillinger er gyldige eller ikke. Utviklingen av å regne i naturfag går fra å bruke enkle metoder for å telle opp, sortere og klassifisere til å kunne vurdere valg av metoder, begreper, formler og måleinstrumenter. Elevene utvikler også regneferdigheter ved å lage mer avanserte framstillinger og ved å bruke regning i faglig argumentasjon.
Delferdighetene av å kunne regne i naturfag
Vi vil her beskrive delferdighetene gjenkjenne og beskrive, bruke og bearbeide, reflektere og vurdere og kommunisere, og hvordan elevene utvikler dem i faget.
Gjenkjenne og beskrive
Å gjenkjenne og beskrive i naturfag vil være å gjenkjenne problemer eller situasjoner i faglige kontekster som kan undersøkes ved hjelp av regning. Dette kan være relatert for eksempel til det å formulere spørsmål og foreslå hypoteser om naturfaglige fenomener.
I naturfag kan elevene få presentert data eller samle inn data selv, og da handler denne delferdigheten blant annet om at de må kunne gjenkjenne matematikken i tallmaterialet. Elevene kan for eksempel undersøke været ved å måle temperatur og nedbør. Å utforme regneuttrykk knyttet til en slik måling, eller velge en formålstjenlig representasjon, for eksempel et diagram, for å vise resultatene av målingen, er en del av det å gjenkjenne og beskrive.
Bruke og bearbeide
For å besvare naturfaglige spørsmål må elevene utføre beregninger. Å utføre beregninger er det mange forbinder med å regne som grunnleggende ferdighet. Beregninger er en del av delferdigheten bruke og bearbeide, men det er bare én av i alt tre delferdigheter av å kunne regne som grunnleggende ferdighet som måles i nasjonale prøver i regning.
Innenfor naturfag handler delferdigheten bruke og bearbeide også om å være i stand til å samle inn data, organisere data og presentere funn. Ut fra eksemplet med registrering av værdata kan det blant annet være naturlig å foreta beregninger for sentralmål og spredningsmål for elever på mellomtrinnet og ungdomstrinnet, mens yngre elever kan framstille resultatet av målingene i et diagram.
Reflektere og vurdere
I faget naturfag møter elevene mange tall og størrelser. Det kan være tall og resultater fra egne beregninger og undersøkelser, tall presentert i en lærebok eller resultater som medelever presenterer. Å tolke tall og resultater og sette dem i perspektiv, er en viktig del av å reflektere og vurdere i naturfag. Påstander som «en enkelt kjempespringfrøplante kan produsere 4000 frø», «ifølge prognosene vil den årlige middeltemperaturen i Oslo være 8,87 °C i 2050» eller «den internasjonale romstasjonen beveger seg med en hastighet på 28 000 km/h», krever ofte at vi går inn i tallmaterialet og setter det i perspektiv for at elevene skal forstå påstandene. Å tolke disse tallene og resultatene vil i mange tilfeller være å prøve å «se bak tallene» og eksemplifisere et tallmateriale som gir samme resultat. En slik tilnærming kan være: «Hva er middeltemperaturen i Oslo i dag, og hvordan kan middeltemperaturen per måned i Oslo bli, dersom middeltemperaturen for hele året skal bli 8,87 °C?» Litt avhengig av konteksten vil det berøre mange av kjerneelementene i faget, og utvikle elevenes faglige kompetanse.
Kommunisere
Elevene må ofte formulere hypoteser og modeller. Dette må komme til uttrykk både muntlig og skriftlig. Elevene må kunne bruke begreper om energi, stoffer og partikler når de skal forklare vår fysiske verden. De må også kunne skrive og formulere rapporter og bruke ulike representasjoner, som for eksempel visuelle framstillinger, for å forklare og begrunne på en oversiktlig og informativ måte.
Aktiviteter som utvikler elevenes grunnleggende ferdighet i å kunne regne
Her finner du aktiviteter som utvikler elevenes grunnleggende ferdigheter i å kunne regne. Aktivitetene ivaretar fagets egenart og tar utgangspunkt i kompetansemål i naturfag.
Utforske et naturnærområde
Flere av kompetansemålene i naturfag handler om at elevene skal kunne oppleve naturen til ulike årstider og reflektere over hvordan naturen er i endring. Ved gjentatte besøk av et naturnærområde gjennom året kan elevene observere temperatur, vekster, dyreliv, spor og sportegn og registrere resultatene. Å planlegge en slik prosess som innebærer å innhente, bearbeide og framstille data, handler mye om hva det å kunne regne i naturfag er definert som.
Kompetansemål i naturfag, LK20, 4. trinn:
- undre seg, stille spørsmål og lage hypoteser og utforske disse for å finne svar
- bruke tabeller og figurer til å organisere data, lage forklaringer basert på data og presentere funn
- utforske et naturområde og drøfte bærekraftig bruk av området
Kompetansemål i naturfag, LK20, 7. trinn:
- stille spørsmål og lage hypoteser om naturfaglige fenomener, identifisere variabler og samle data for å finne svar
- skille mellom observasjoner og slutninger, organisere data, bruke årsak-virkning-argumenter, trekke slutninger, vurdere feilkilder og presentere funn
Kompetansemål i naturfag, LK20, 10. trinn:
- stille spørsmål og lage hypoteser om naturfaglige fenomener, identifisere avhengige og uavhengige variabler og samle data for å finne svar
- analysere og bruke innsamlede data til å lage forklaringer, drøfte forklaringene i lys av relevant teori og vurdere kvaliteten på egne og andres slutninger
Sammenligning og sortering: ordning og klassifisering
En annen aktivitet i naturnærområdet kan være å sette fallfeller for småkryp. Her vil også regneutfordringen bestå i å telle og klassifisere, men også å sortere og klassifisere småkrypene, samt presentere resultater. Utviklingen av den grunnleggende ferdigheten å kunne regne i naturfag går fra å bruke enkle metoder for å telle opp, sortere og klassifisere til å kunne vurdere valg av metoder, utvikle matematiske modeller og bruke resultatene til å si noe om en bestand.
Å se etter sammenhenger er en måte å forstå verden på, og i naturfag ser vi spesielt på sammenhenger i naturen. Regning som grunnleggende ferdighet bidrar med hvordan vi kan undersøke sammenhenger. Sammenligning er grunnleggende for å kunne finne sammenhenger. Når vi sammenligner, ser vi etter likheter og forskjeller for å skape orden. Å kunne sortere handler om å sammenligne og ordne etter klasser eller ordning. Ordning og klassifisering er forutsetninger for å utforske en rekke naturfaglige tema. Ordning handler om rekkefølgen og fokuserer på det som er forskjellig, for eksempel å sortere dyr fra størst til minst. Klassifisering handler om å finne det som objekter har til felles, og som skiller dem fra andre.
Geologer klassifiserer når de observerer om steiner er prikkete, stripete eller «lag på lag», og sorterer steinene i ulike klasser etter disse egenskapene. Klassen steinene tilhører, forteller om bergartens mønster og historie. I tillegg må geologen undersøke steinene innenfor en klasse, og se om de kan klassifiseres i undergrupper. Ut fra likheter og ulikheter kan geologer og elever identifisere bergarten.
En nærmere beskrivelse av aktiviteten finner du her (Naturfag.no).
Kompetansemål i naturfag, LK20, 7. trinn:
- gjøre rede for hvordan organismer kan deles inn i hovedgrupper, og gi eksempler på ulike organismers særtrekk
Se også kompetansemål i aktiviteten «Utforske et naturnærområde».
Utforske en elektrisk krets
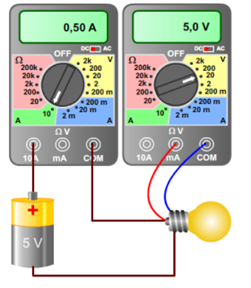
La elevene utforske ved å koble flere batterier i serie, lese av verdiene på apparatene, sette verdiene inn i formelen og regne ut effekten. Deretter kan motstanden endres ved å koble flere lyspærer i serie, lese av på apparatene og regne ut effekten på nytt. Lek og utforsking kan bidra til at elevene ser både sammenhengen mellom de tre begrepene i formelen og sammenhengen mellom benevningene.
Når elevene er blitt fortrolige med å undersøke ulike effekter ved å variere spenning og strøm, er det naturlig også å komme inn på sammenhengen mellom spenning, strøm og motstand. Det må kobles til variasjonen av lyspærer og antall batterier i en krets, og det å sette verdier inn i formlene og regne ut. Øvelse er nødvendig for å bli vant til å regne med formler.
Refleksjonsspørsmål kan være:
- Hva skjer med effekten når spenningen dobles, men antall lyspærer er konstant? Hvordan kan du se at effekten endres?
- Hva skjer med strømmen når antall lyspærer dobles, mens antall batterier er konstant? Hvordan kan du se at effekten endres?
- Hvorfor er 1 W = 1 VA?
Kompetansemål i naturfag, LK20, 7. trinn:
- utforske elektriske og magnetiske krefter gjennom forsøk og samtale om hvordan vi utnytter elektrisk energi i dagliglivet
Fordamping gir avkjøling
Dette er en praktisk aktivitet hentet fra Naturfagsenterets nettside naturfag.no. I aktiviteten skal elevene gjennomføre en digital datalogging for å se på det naturfaglige fenomenet at fordamping gir avkjøling. I etterkant av dataloggingen kan elevene anvende den grunnleggende ferdigheten å kunne regne for å svare på refleksjonsspørsmål.
Aktiviteten finner du her (Naturfag.no)
Kompetansemål i naturfag, LK20, 7. trinn:
- stille spørsmål og lage hypoteser om naturfaglige fenomener, identifisere variabler og samle data for å finne svar
- skille mellom observasjoner og slutninger, organisere data, bruke årsak-virkning-argumenter, trekke slutninger, vurdere feilkilder og presentere funn
- utforske faseoverganger og kjemiske reaksjoner og beskrive hva som kjennetegner dem
- bruke partikkelmodellen til å forklare faseoverganger og egenskapene til faste stoffer, væsker og gasser
Kompetansemål i naturfag, LK20, 10. trinn:
- stille spørsmål og lage hypoteser om naturfaglige fenomener, identifisere avhengige og uavhengige variabler og samle data for å finne svar
- analysere og bruke innsamlede data til å lage forklaringer, drøfte forklaringene i lys av relevant teori og vurdere kvaliteten på egne og andres utforskinger
Tyngdekraft og luftmotstand
Dette undervisningsopplegget synliggjør bruken av regning som grunnleggende ferdighet i naturfag. Her blir regning brukt for å studere masse, tyngdekraft og luftmotstand. Opplegget er laget etter revidert bakgrunnsdokument.
- Årstrinn: 8-10
- Tidsbruk: 60 minutter
Aktuelle kompetansemål
Mål for opplæringen er at eleven skal kunne
- stille spørsmål og lage hypoteser om naturfaglige fenomener, identifisere avhengige og uavhengige variabler og samle data for å finne svar
- analysere og bruke innsamlede data til å lage forklaringer, drøfte forklaringene i lys av relevant teori og vurdere kvaliteten på egne og andres utforskinger
Nærmere beskrivelse av opplegget
Utstyr
- muffinsformer
- stoppeklokke
- målebånd
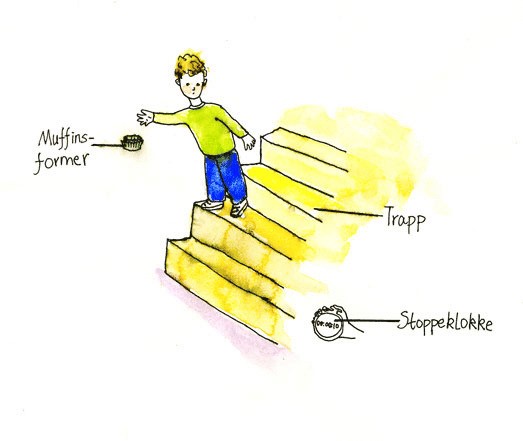
Dersom en lar en muffinsform falle fritt, oppnår den konstant fart veldig raskt. Den daler pent ned til gulvet. Det betyr at luftmotstanden raskt blir lik tyngden til formen, slik at kraften nedover blir lik kraften oppover. Men hva har massen å si?
- Presentasjon av aktiviteten: Velg en bestemt høyde, for eksempel kateteret. Læreren, gjerne med hjelp av elever, slipper en muffinsform, og måler tiden det tar for en muffinsform å treffe gulvet. Så gjør det samme med to muffinsformer i hverandre.
- Formulere hypoteser: Kan vi bruke resultatene fra presentasjonen til å forutsi hvor lang tid fire muffinsformer bruker ned til gulvet? Eller seks muffinsformer? Her kan det være aktuelt for læreren å diskutere begrepet masse med elevene, slik at de knytter massebegrepet inn i hypotesene de lager. Begrepene tyngdekraft og luftmotstand kan også være aktuelt å diskutere, avhengig av elevenes forkunnskaper. Alle elevene skal lage hypoteser om hvordan de tror resultatene vil bli.
- Innhenting av data: Elevene skal jobbe i grupper på 2-4 elever. Nå skal de selv velge en høyde som de skal slippe muffinsformene fra. De skal måle tiden det tar for flere muffinsformer å nå gulvet. De må gjøre mange målinger med ulikt antall muffinsformer som er sluppet fra samme høyde. Elevene må underveis dokumentere målingene, og finne en måte å vise resultatene av målingene til resten av klassen. Her er en grafisk framstilling å foretrekke, men la hver gruppe vise det på sin egen måte. Dersom elevene ser at andre grupper har en mer effektiv måte å vise det på enn sin egen, kan de oppdage verdien av den måten å framstille resultatene på.
- Oppsummerende samtale: Læreren leder en oppsummerende samtale i plenum der elevene reflekterer over erfaringene. Hvorfor blir farten konstant etter kort tid? Hva har massen å si for falltiden? Hva har massen å si for luftmotstanden? Hvordan kan vi bruke erfaringer til å forme hypoteser? Dette danner bakteppe for de faglige begrepene som ligger til grunn for opplegget.
- Videre arbeid: Opplegget kan ligge til grunn for en rapport elevene skal skrive. Dessuten kan opplegget bygges videre til andre problemstillinger. For eksempel: hva vil skje dersom vi har samme antall muffinsformer, men øker fallhøyden? Hvor mye må en øke høyden dersom en ønsker å få fire muffinsformer til å treffe gulvet samtidig som en slipper én muffinsform fra utgangshøyden?
Faglig forklaring
Det er mulig å vise matematisk at fallhøyden innenfor et gitt tidsrom er proporsjonal med kvadratroten av massen. Det vil si at fire muffinsformer vil treffe gulvet samtidig som en form når de slippes samtidig, dersom vi slipper de fire formene fra en dobbel så stor høyde (kvadratroten av fire er to; det vil si dobbelt så stor høyde). Kvadratroten av tre er ca 1,7. Slipper vi en form fra 1 meters høyde, må tre former i hverandre slippes fra ca 1,7 meter. De skal altså treffe gulvet samtidig.
Vurdering
Målet for timen må være tydelig for elevene. Kompetansemålene må tolkes og analyseres av læreren, som videre må formulere læringsmål for elevene slik at de forstår hva som forventes av dem. I dette opplegget kan det for eksempel være å forstå begrepet fart og hvilke faktorer som påvirker farten til et legeme, slik som masse og luftmotstand. Underveis i opplegget må elevene få tilbakemeldinger på kvaliteten på arbeidet sitt og råd om videre arbeid. Dette er spesielt aktuelt med tanke på formuleringen av hypotesene. Hvordan innhentingen av data skjer er også viktig at elevene får tilbakemelding på slik at dataene gir svar på det de forsøker å finne ut av. Det bør skje på en slik måte at elevene selv blir involvert i eget arbeid og utvikling. Det kan for eksempel gjøres ved å stille reflekterende spørsmål direkte til gruppene. Eksempler på slike spørsmål står i beskrivelsen av opplegget
Helhetlig problemløsningsprosess
Gjenkjenne og formulere
I denne aktiviteten må elevene gjenkjenne muligheten til å bruke forhold til å formulere en matematisk problemstilling som handler om forholdet mellom slipphøyden og tiden det tar før muffinsformen treffer bakken. Her bør også elevene gjenkjenne muligheten til å benytte seg av grafer og/eller tabeller til å organisere resultatene fra forsøket.
Bruke og bearbeide
Elevene må bruke og bearbeide resultatene fra målingene slik at de kommer fram til en matematisk løsning. I dette tilfellet betyr det for eksempel at elevene må sette tallene inn i tabellen på riktig måte slik at de kan analysere tabellen i etterkant og se hvilken innvirkning antall muffinsformer har på tiden.
Reflektere og vurdere
Elevene må til slutt reflektere og vurdere om det matematiske svaret er en god løsning på det virkelige problemet. For eksempel kan man tenke seg at elevene ser en utvikling i målingsresultatene som viser at 2 muffinsformer faller dobbelt så fort som 1 muffinsform, 4 muffinsformer faller dobbelt så fort som 2 muffinsformer, osv. Da må elevene først resonnere seg fram til om det er en mulig løsning i forhold til virkeligheten. Deretter må de se om denne utviklingen faktisk stemmer ved å gjøre nye målinger.
Kommunisere
Kommunikasjon er gjennomgående i hele problemløsningsprosessen. I dette opplegget må elevene i gruppene kunne formidle til hverandre det matematiske innholdet som er nødvendig for å oppnå kompetansemålene. Videre må elevene kommunisere skriftlig når de formulerer problemstilling som skal gi svar på om massen påvirker muffinsformene, og i så fall på hvilken måte. Til slutt må de kommunisere hva de har kommet fram til, enten gjennom en skriftlig innlevering eller muntlig presentasjon.
Idéen er hentet fra Naturfagsenteret
Massetetthet til stoffer
I dette undervisningsopplegget skal elevene tolke tabeller og annen relevant informasjon for å beregne massetetthet og finne ut hvordan stoffers egenskaper avhenger av massetettheten.
Aktuelle kompetansemål
Mål for opplæringen er at eleven skal kunne
- stille spørsmål og lage hypoteser om naturfaglige fenomener, identifisere avhengige og uavhengige variabler og samle data for å finne svar
Oppgave/forsøk til elevene
- Finn ut hvordan egenskapene til stoffer avhenger av massetettheten. Dere må beregne massetettheten, bruke tabellen og skrive rapport. Dere har fem like store terninger laget av forskjellige stoffer
- Formuler en hypotese om hvilke terninger som skal flyte og hvilke som skal synke i vannet.
- Test hypotesen ved å kaste gjenstander i vannet. Noter resultatene.
- Ved å bruke vekt, målesylinder, kalkulator og en tabell over tettheten til forskjellige stoffer, finn ut hvilke stoffer terningene er laget av.
- Diskuter hvordan massetettheten til stoffene bestemmer flyteegenskapene. Formuler en konklusjon.
- Skriv en rapport hvor du setter opp hypotesen, beskriver gangen i forsøket med nødvendige beregninger og vurderinger, samt formulerer en konklusjon. Rapporten skal inneholde en tabell som viser funnene dere gjør oversiktlig.
Hvordan kommer regning til syne i undervisningsopplegget?
Dette undervisningsopplegget handler om å bruke regning i faglig argumentasjon. Det innebærer å bruke begreper, metoder, måleinstrumenter og formler for å svare på en problemstilling. I tillegg skal elevene bruke framstilinger som for eksempel en tabell når de dokumenterer arbeidet oversiktlig.
Vurdering
Før en starter, presenterer læreren aktiviteten for elevene og svarer på oppklarende spørsmål. Arbeidet foregår i større eller mindre grupper. Eleven må være innforstått med hva han skal lære ved hjelp av denne aktiviteten og forstå hva som forventes av ham. Lærer støtter eleven i gjennomføringen av aktiviteten ved å komme med konkrete tilbakemeldinger på utforming av hypotese og faglige argumenter underveis i arbeidet. Lærer vurderer videre elevens kompetanse ved gjennomføring av praktisk øvelse både når det gjelder nøyaktighet av målinger og bruk av formler og tabeller. Den skriftlige framstillingen kan bli vurdert av eleven selv, medelev og lærer i henhold til kjente vurderingskriterier som gjelder naturfaglig rapport. Eleven kan med fordel involveres i eget læringsarbeid ved å vurdere sin egen rapport før lærer gjør sin vurdering og kommer med råd om forbedringer.
Helhetlig problemløsningsprosess
Gjenkjenne og beskrive
Elevene må gjenkjenne muligheten til å benytte regning for å finne massetettheten til de ulike stoffene. I tillegg må de klare å plukke ut relevant til en tabell i rapporten de skal skrive.
Bruke og bearbeide
Elevene skal beregne massetettheten til gjenstander. De må kunne bruke formelen fleksibelt og bruke riktig benevning. I tillegg må de kunne lage en informativ tabell basert på de resultatene de får underveis i forsøket.
Reflektere og vurdere
Elevene må reflektere og vurdere i forhold til om de utregningene de gjør stemmer med utprøvingen i punkt 2. Er det for eksempel slik at de ulike stoffenes massetetthet stemmer med de observerte funnene i punkt 2?
Kommunikasjon
Elevene må kommunisere gjennom hele oppgaven. Først formulerer de sin egen hypotese, for så å sjekke om denne stemte eller ikke. Under utregning av massetetthet må elevene kunne forklare og begrunne det de gjør, og til slutt skal de i rapporten sin sammenfatte hele forsøket på en oversiktlig og informativ måte. Her skal de blant annet kommunisere ved hjelp av en tabell.