Kva kjenneteiknar god matematikkundervisning?

Oppgåva på Matematikksenteret er å fremje ei forskingsbasert forståing av god læring og undervisning i matematikk, ein «ambisiøs matematikkundervisning». Det er ei undervisningsform som har som mål å utvikle forståinga og engasjementet til elevane, og dessutan kompetansen deira til å berekne, nytte og resonnere. Dette er viktige trekk som blir spegla i kjerneelementa.
Ambisiøs matematikkundervinsing (Ambitious teaching) byggjer på ei aukande mengd forsking frå dei siste tretti åra, der undersøkjande arbeidsmetodar står sentralt for elevane.
Kva betyr det i praksis?
I ein undersøkjande og ambisiøs undervisningskontekst set læraren opp læringsmåla, men lèt elevane sjølv utforske problema for å finne mønster og system. Elevane driv aktiv matematisk utforsking, og diskuterer eigne løysingsstrategiar med kvarandre. Om elevane tek feil, blir det rekna som ein naturleg del av læringsprosessen. Når elevane får lov til å utforske eit felt og diskutere korleis dei tenkjer - med kvarandre - oppdagar dei at matematikk slett ikkje er eit fag som berre består av å hugse kva læraren har sagt. I staden blir det til eit spennande og aktivt fag som består av utforsking på elevane sine eigne premissar.
"Dei fire prinsippane"
Ambisiøs undervisning byggjer på nokre sentrale prinsipp for arbeidet til læraren, og desse må sjåast i samanheng med kvarandre. Ambisiøs matematikkundervisning kan vere krevjande – men gøy! – og vi oppmodar alle lærarar til å bruke tid på å utvikle sin eigen praksis.
Matematikk som gir meining
Dette prinsippet handlar om at læraren:
- prøver å forstå korleis matematiske tema kan gi meining for elevane
- førebur aktivitetar på ein måte som gjer at elevane får ansvar for å arbeide med seriøs matematikk
- gir elevane høve til å resonnere
Læraren må med andre ord ta utgangspunkt i tenkinga til elevane. Dei må stille spørsmål, observere og tolke resonneringa, språket og argumenta til elevane og, basert på dette, tilpasse undervisninga. Målet er å fremje læringa til elevane.
Deltaking og likeverdig tilgang
Undervisninga skal gi alle elevane høve til å arbeide med utfordringar i matematikk, og alle får likeverdig tilgang til å lære.
Læraren skal ta utgangspunkt i at alle elevar, uansett dei noverande ferdigheitene deira eller kompetanse, er i stand til ambisiøs læring. Han prøver å differensiere undervisninga på måtar som gjer at alle elevar, med ulike bakgrunnar og læringsspor, kan ha framgang i matematikk.
Tydelege læringsmål
I ei ambisiøs matematikkundervisning, planlegg læraren aktivitetane og gjennomfører dei med tydelege læringsmål i sikte. Desse læringsmåla er ofte knytt til dei sentrale ideane (big ideas) i matematikk. Læraren må vere godt kjend med det matematiske innhaldet, på ein slik måte at han kan hjelpe elevane i læringsprosessen.
Kunnskap om elevane som lærande
Dette prinsippet handlar om at lærarar må kjenne dei individuelle styrkane til elevane, vanar, og problem, så vel som kven elevane er som lærande:
- kva dei kan og håpar å kunne
- korleis dei arbeider best
- korleis dei ser på seg sjølv og eiga læring
Kjenneteikn på ei ambisiøs matematikkundervisning
I tillegg til desse prinsippa, så finst det nokre tydelege kjenneteikn som går igjen i ei ambisiøs matematikkundervisning:
- Elevane arbeider med oppgåver og aktivitetar som fremjar resonnering og problemløysing.
- Elevane har mange høve til å samarbeide, og deltek i matematiske samtalar.
- Elevane utviklar eigne løysingsstrategiar.
- Læraren etablerer eit positivt affektivt klasseromsmiljø ved å behandle elevane med respekt, lytte til ideane deira og verdsetje dei faglege bidraga deira.
- Læraren fremjar djupnelæring og forståing i matematikk.
- Læraren kjem med konkrete og konstruktive tilbakemeldingar som utfordrar elevane.
- Feil blir rekna som ein del av læringsprosessen.
Kva er matematisk kompetanse?
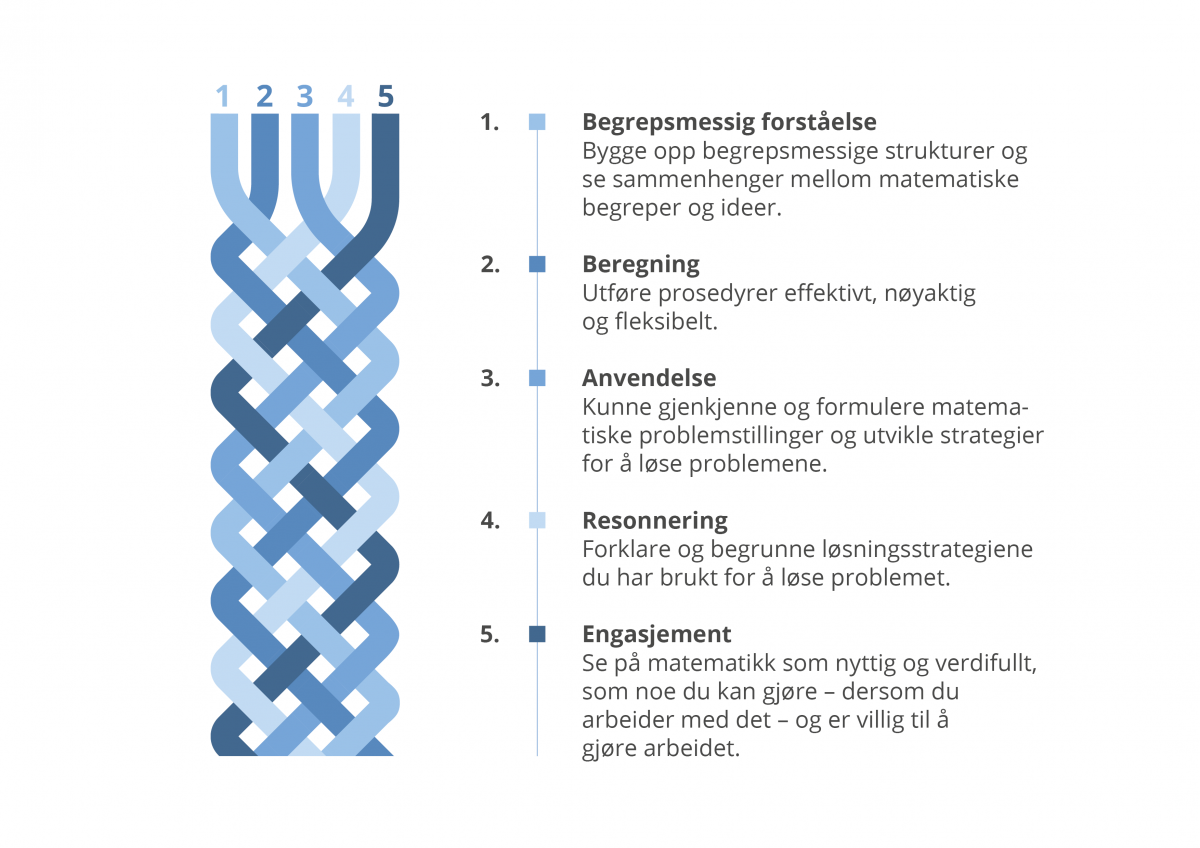
Forsking viser at ambisiøs matematikkundervisning fremjar matematisk kompetanse. Men kva ligg eigentleg i omgrepet «matematisk kompetanse»? Ifølgje «Trådmodellen» (Kilpatrick, Swafford og Findell, 2001) blir matematisk kompetanse beskriven som samansett av fem komponentar: Forståing, berekning, bruk, resonnering og engasjement. Alle komponentane er tett samanfletta og avhengige av kvarandre. Ved å arbeide med alle fem komponentane, vil elevane utvikle ein solid, varig, fleksibel og relevant kompetanse i matematikk. Dei fem komponentane omfattar alle kjerneelementa i læreplanen, LK20.
Etterutdanning i Ambisiøs matematikkundervisning
MAM er Matematikksenterets etterutdanningsprogram i ambisiøs matematikkundervisning. I tillegg er alle matematikkmodular i Realfagsløyper utvikla med utgangspunkt i ambisiøs matematikkundervisning.
Det blir brukt mange namn og nemningar som beskriv ei undervisning som inkluderer fleire av desse elementa, og som har store likskapar med Ambisiøs matematikkundervisning. Døme på dette er «russisk matematikkundervisning», «dialogbasert undervisning», og ikkje minst «Undersøkjande/utforskande undervisning».
Mattelist.no - ambisiøse aktivitetar
Undersøkjande arbeidsmetodar står sentralt i ambisiøs matematikkundervisning. På Mattelist.no finn du aktivitetar som er utvikla for å skape betre forståing og engasjement i matematikk, og inneheld lærarrettleiingar som er utarbeidde med utgangspunkt i ambisiøs matematikkundervisning.
Kjelder: National Council of Teachers of Mathematics. (2014). Principles to Actions. Ensuring Mathematical Success for All. Reston, VA: Author.