Modul 3 - Input

Hensikt
Matematikk
- Utforske vinkler i regulære mangekanter.
- Tegne diagonaler i mangekanter.
- Beregne avstand mellom punkter (for ungdomstrinnet).
Programmering
- Input – blokken spør tar i bruk informasjon fra brukeren.
Oversikt over nye blokker i denne modulen
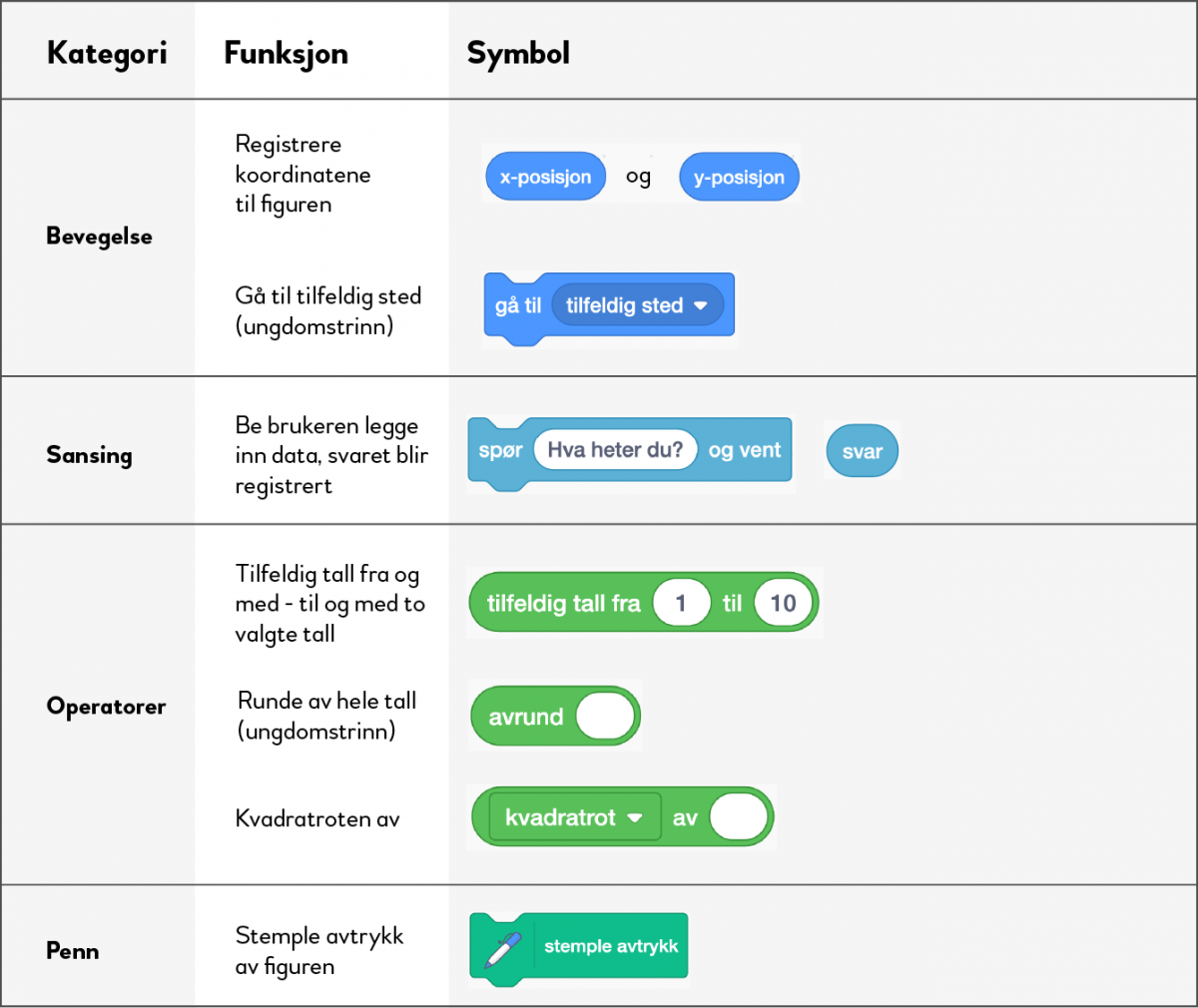
Kort oversikt
Modulen består av tre deler og bygger videre på arbeidet med kvadrater. Modulen introduserer noen få nye blokker, hvor den viktigste handler om input. Elevene får også tid til å repetere bruken av sentrale blokker, som for eksempel variabler og beregninger. DEL 1 og 2 handler både om å tegne regulære mangekanter og å lage mønster med mangekanter , i tillegg til å lage mønster ved å stemple figuren. DEL 3 handler om å tegne diagonaler i kvadrater og regulære femkanter med tilfeldig størrelse og orientering. Denne delen har et tillegg for ungdomstrinnet om å beregne avstander slik at man kan finne lengden til diagonalene. Det forutsetter at elevene er kjent med Pytagoras' setning.
Del 1 - vinkler i rektangulære mangekanter
Elevene får se denne kodeblokken som de kjenner fra før (arbeidsark 03a):
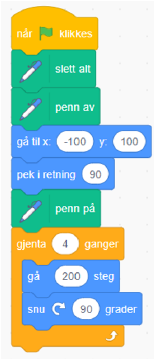
Be elevene diskutere hvilke verdier som må endres hvis programmet skal tegne en regulær (likesidet) trekant. La dem prøve ut forslagene sine. Når de har funnet verdier som passer, noterer de verdiene. Mange vil nok støte på dette problemet: Hvorfor blir det ikke en trekant når vi snur 60 grader? La dem selv finne ut hvor mange grader de må rotere i hvert hjørne. Vent med en begrunnelse til elevene har erfaringer nok til å lete etter og kanskje finne en forklaring selv.
Elevene får så endre verdier slik at figuren blir en regulær femkant, sekskant og så videre og lager en oversikt på resultatene de kommer til. En tabell vil være nyttig:
| Antall kanter | Vinkel (i grader) |
|---|---|
| 3 | 120 |
| 4 | 90 |
| 5 | 72 |
| 6 | 60 |
| ... | ... |
Utfordring for elevene
Finn en sammenheng mellom vinkelen man må rotere og antall sider. Hvorfor er det slik? Hva skjer med mangekanten om vi velger et stort antall sider, for eksempel 12?
Kommentar
Eksempel med regulær trekant.
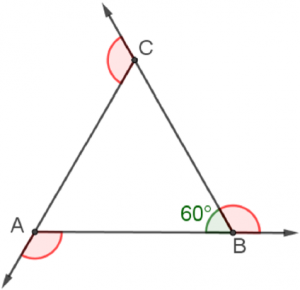
Dette skjer når trekanten blir tegnet:
- Man starter i punkt A og peker i retning B.
- I B må rotasjonen være så stor at det blir 60 grader "inne i" trekanten. Da peker pila i retning mot C. Rotasjonsvinkelen er markert rød.
- Når denne rotasjonen er utført tre ganger, peker pila i samme retning som i punkt 1.
Den samlede rotasjonen blir da `360 °`, og hver rotasjon er da `360 °:3 =120 °`
Tilsvarende argument kan man benytte på andre regulære mangekanter.
Input bra brukeren
Når vi har sett sammenhengen mellom antall sider og vinkelen (produktet er 360), kan vi få beregnet rotasjonsvinkelen automatisk. Det kan vi gjøre ved å la elevgrupper prøve å forutsi hva dette programmet gjør og så legge opp til en diskusjon i klassen (arbeidsark 03b).
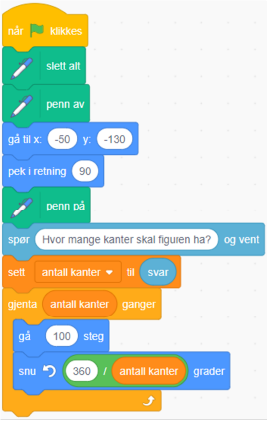
Kommentar
I dette tilfellet er det strengt tatt ikke nødvendig å lage en variabel av svaret når bruken kun gir input til én variabel – her er det antall kanter i mangekanten. Resultatet hadde blitt det samme om variabelen "antall sider" blir utelatt. Blokken "snu" måtte da se slik ut: 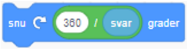 .
.
Hvis brukeren skal legge inn flere svar, må man lage en variabel av hvert svar, så det er en god vane å lage en variabel av tallsvarene brukeren skal gi som input.
Når elevene lager og kjører kodeblokken med ulike antall kantar, oppdager de kanskje at det skjer noe spesielt når antall kanter øker. Årsaken er at mangekanten blir for stor. Mangekanten får ikke plass i resultatvinduet og den blir ikke lukket, slik som på bildet.
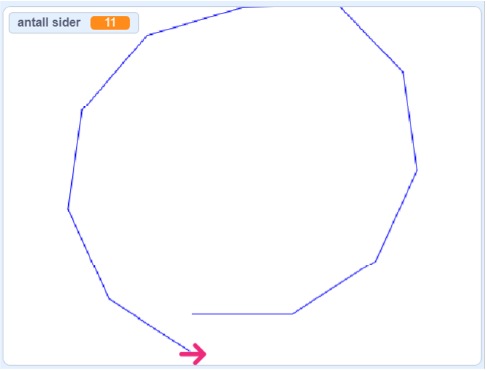
Modifisering
Utfordre elevene på å modifisere kodeblokken slik at de kan få tegnet regulære mangekanter med så mange kanter de ønsker. Disse tre eksemplene viser at det er mulig å få på plass mangekanter med svært mange kanter. De er laget med samme kodeblokk og har hhv. 15, 3 og 360 kanter.
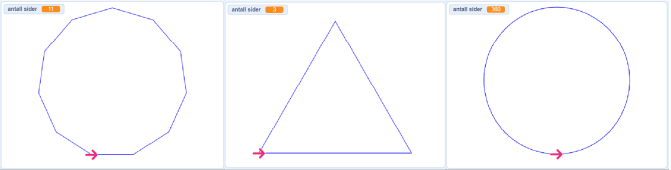
Be elevene sammenlikne de tre mangekantene og dele tanker om hva de må legge inn i kodeblokken for å tilpasse mangekantene til resultatvinduet.
Kommentar
Nøkkelen her er å tilpasse sidelengden til antall kanter i mangekanten. Det kan gjøres ved å lage en ny variabel som kan hete "kantlengde". På bildene er variabelen laget slik:  .
.
Antall kanter bestemmer også hvor pila skal stå når opptegningen begynner. Den må plasseres slik at mangekanten får plass i resultatvinduet. Antall kanter vil også påvirke hvor pila skal plasseres før opptegningen starter. Det kan for eksempel løses ved å sette inn blokken 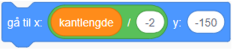 .
.
En ekstra utfordring
Modifiser kodeblokken slik at alle mangekantene med 3-20 kanter blir tegnet på denne måten (arbeidsark 02c).
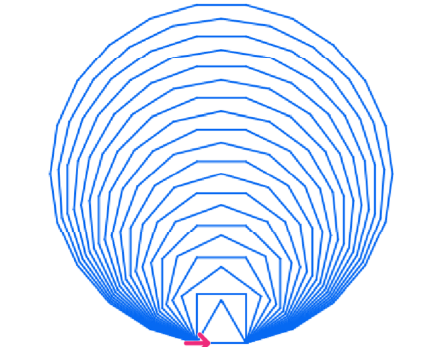
Mønsteret blir mer fargerikt om fargen endres for hver mangekant.
Prøv å starte med: 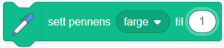 og så endre farge for hver nye mangekant:
og så endre farge for hver nye mangekant:  .
.
Resultatet kan for eksempel bli slik:
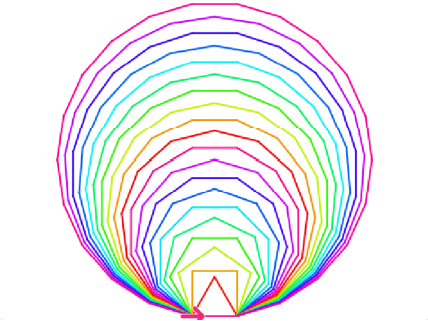
Del 2 - lag mønster med stempel
Så langt er alle tegninger og mønster laget med pennen. Blokken stemple avtrykk, som ligger under penn-verktøyet, gir nye muligheter når man ønsker å lage mønster.
Eksempel
En kodeblokk som lager en regulær femkant, kan modifiseres slik at den lager et stempel i hvert hjørne, uten at pennen tegner linjer. Da må man sørge for at pennen er av. Figuren "Arrow1" er kanskje ikke den beste figuren for å lage et mønster. Figuren "Cat 2" kan være et alternativ.

Spar tid på gjenbruk av kodeblokker!
Når man vil lage et nytt program ved å modifisere en kodeblokk man allerede har laget, kan det gjøres på flere måter, blant annet:
- Lag en kopi av prosjektet.
- Bruk ryggsekken. Ønsker du å bruke en annen figur enn for eksempel "Arrow", er nok det enkleste å bruke ryggsekken. Ryggsekken åpnes når man klikker på Ryggsekk nederst i skjermbildet. Da kan man dra hele kodeblokken man vil gjenbruke ned i ryggsekken. Så må man starte et nytt prosjekt ved å velge "Ny" under "Filer" på menylinjen, hente inn den figuren man ønsker å bruke, og så dra opp kodeblokken fra ryggsekken. Bruk av ryggsekken krever at man er logget inn.
La elevene leke seg med mønster
De blokkene elevene til nå er introdusert for, gir rike muligheter for kreativ utfoldelse, analyse av kodeblokker og algoritmisk tenking.
Den algoritmiske tenkingen kan utvikles og styrkes ved analogt arbeid.
La elevene
- tegne en skisse av det mønsteret de ønsker å lage en kodeblokk for (eller velge noe som likner et av forslagene) – bruk gjerne kopioriginalen 01c Koordinatsystem.
- lage en algoritme hvor de beskriver hvordan kodeblokken skal bygges opp (pseudokode*).
- lage eller modifisere en kodeblokk med utgangspunkt i pseudokoden.
Pseudokode
*Eksempel på pseudokode til mønster D nedenfor. Kopioriginal 03 Reg Mang 4.
- Start nede i venstre hjørne
- Lag en regulær sekskant med stempel av figuren i hvert hjørne
- Flytt til høyre og lag en ny sekskant slik at det blir åtte sekskanter på ei linje
- Endre farge på figuren
- Flytt til start på ei ny linje med sekskanter over den linjen som ble laget
- Gjenta punktene 3, 4 og 5 så mange ganger det er plass til
Eksempler til inspirasjon

Kommentar
Noen figurer kan skifte farge, for eksempel "Ball" og "Snowflake". Noen kan skifte utseende, for eksempel "Dove". Ønsker man slike effekter, må man velge blokker under Utseende.
Med ballen kan man bruke blokken 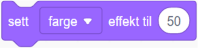 , som er benyttet i mønster G. Ønsker man å endre fargen, kan man bruke blokken
, som er benyttet i mønster G. Ønsker man å endre fargen, kan man bruke blokken 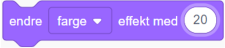 .
.
Dette tilsvarer de to blokkene vi finner under penn-verktøyet:  og
og  .
.
Duen i mønster F har to drakter, dove-a og dove-b: 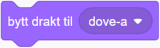 ,
, 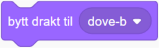 . Hver linje med duer starter med dove-a. For hver forflytning i en linje bytter figuren drakt med denne blokken:
. Hver linje med duer starter med dove-a. For hver forflytning i en linje bytter figuren drakt med denne blokken:  .
.
Del 3 - diagonaler
Introduksjon av blokkene  ,
, 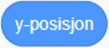 og
og 
Figuren viser starten på en kodeblokk som skal tegne et kvadrat og en diagonal i kvadratet. Kvadratet har en tilfeldig plassering og orientering i resultatvinduet.
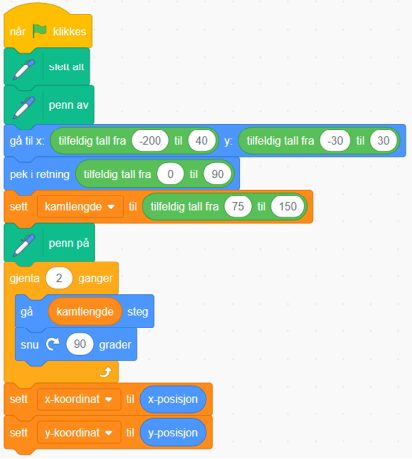
Be elevene studere kodeblokken og tenke over hva spesielt de to siste blokke gjør. La elevene fullføre kodeblokken slik at programmet tegnet et kvadrat med en diagonal.
Kommentar
Blokkene  og
og  sikrer at kvadratet blir liggende innenfor resultatvinduet. Om man bruker blokkene
sikrer at kvadratet blir liggende innenfor resultatvinduet. Om man bruker blokkene 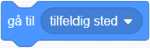 og
og  , som gir større grad av tilfeldighet, risikerer man at kvadrat blir deformert.
, som gir større grad av tilfeldighet, risikerer man at kvadrat blir deformert.
Beregne avstand - for ungdomstrinnet
Start med den analoge aktiviteten i arbeidsark 03f Beregne avstand.
La elevene lage en kodeblokk som beregner avstanden mellom to tilfeldige punkter. Tilfeldige punkter kan velges med blokken  .
.
Utfordre elevene på å beregne lengden til
- diagonalen i det tilfeldige kvadratet
- en diagonal i en tilfeldig regulær femkant
- en diagonal i en annen regulær mangekant.
Kommentar
Avstandene som blir beregnet med Pytagoras setning kan ha mange desimaler, for eksempel  . Hvis beregningen legges inn i blokken
. Hvis beregningen legges inn i blokken  , blir resultatet
, blir resultatet  .
.